
【题目】
(1)求与点P(3,5)关于直线l:x-3y+2=0对称的点P′的坐标.
(2)已知直线l:y=-2x+6和点A(1,-1),过点A作直线l1与直线l相交于B点,且|AB|=5,求直线l1的方程.
【答案】
(1)解:设P′(x0 , y0),则kPP′= ![]() ,PP′中点为
,PP′中点为 ![]() .
.
∴ 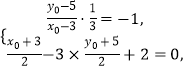 解得
解得 ![]() ∴点P′坐标为(5,-1)
∴点P′坐标为(5,-1)
(2)解:当直线l1的斜率不存在时,方程为x=1,此时l1与l的交点B的坐标为(1,4).|AB|= ![]() 符合题意.
符合题意.
当直线l1的斜率存在时,设为k,则k≠-2,∴直线l1为y+1=k(x-1),
则l1与l的交点B为 ![]() ,
,
∴|AB|= ![]() ,
,
解得k=- ![]() ,∴直线l1为3x+4y+1=0.
,∴直线l1为3x+4y+1=0.
综上可得l1的方程为x=1或3x+4y+1=0
【解析】(1)点关于直线的对称点应满足:点与其对称点连线与直线垂直,其中点在直线上,由此得到对称点坐标的方程组求解;
(2)设出所求直线的方程,求出与已知直线的交点坐标,由|AB|=5求出k,得到直线方程,要注意斜率不存在的情况。


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】已知α,β,γ是不重合的平面,a,b是不同的直线,则下列说法正确的是( )
A.“若a∥b,a⊥α,则b⊥α”是随机事件
B.“若a∥b,aα,则b∥α”是必然事件
C.“若α⊥γ,β⊥γ,则α⊥β”是必然事件
D.“若a⊥α,a∩b=P,则b⊥α”是不可能事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线x2=4y焦点为F,点A,B,C为该抛物线上不同的三点,且满足 ![]() +
+ ![]() +
+ ![]() =
= ![]() .
.
(1)求|FA|+|FB|+|FC|;
(2)若直线AB交y轴于点D(0,b),求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有除颜色外其余均相同的12个小球,从中随机取出1个球,取出红球的概率为 ![]() ,取出黑球的概率为
,取出黑球的概率为 ![]() ,取出白球的概率为
,取出白球的概率为 ![]() ,取出绿球的概率为
,取出绿球的概率为 ![]() .求:
.求:
(1)取出的1个球是红球或黑球的概率;
(2)取出的1个球是红球或黑球或白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x3+a|x2﹣1|,a∈R,则对于不同的实数a,则函数f(x)的单调区间个数不可能是( )
A.1个
B.2个
C.3个
D.5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点为O极点,以x轴正半轴为极轴,圆C的极坐标方程为ρ=4 ![]() .
.
(1)将圆C的极坐标方程化为直角坐标方程;
(2)过点P(2,0)作斜率为1直线l与圆C交于A,B两点,试求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com