
已知直线l:y=x+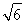 ,圆O:x2+y2=5,椭圆E:
,圆O:x2+y2=5,椭圆E: =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=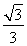 ,直线l被圆O截得的弦长与椭圆的短轴长相等.
,直线l被圆O截得的弦长与椭圆的短轴长相等.
(1)求椭圆E的方程;
(2)过圆O上任意一点P作椭圆E的两条切线,若切线都存在斜率,求证:两条切线的斜率之积为定值.
(1)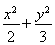 =1(2)两条切线的斜率之积为常数-1
=1(2)两条切线的斜率之积为常数-1
【解析】(1)设椭圆的半焦距为c,圆心O到直线l的距离d=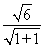 =
= ,∴b=
,∴b=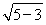 =
=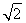 ,
,
由题意,得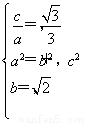 ∴a2=3,b2=2.
∴a2=3,b2=2.
∴椭圆E的方程为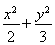 =1.
=1.
(2)设点P(x0,y0),过点P的椭圆E的切线l0的方程为y-y0=k(x-x0),
联立直线l0与椭圆E的方程,得
消去y,得(3+2k2)x2+4k(y0-kx0)x+2(kx0-y0)2-6=0,
∴Δ=[4k(y0-kx0)]2-4(3+2k2)[2(kx0-y0)2-6]=0,整理,得(2-x)k2+2kx0y0-(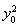 -3)=0,设满足题意的椭圆E的两条切线的斜率分别为k1,k2,
-3)=0,设满足题意的椭圆E的两条切线的斜率分别为k1,k2,
则k1·k2=-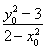 .
.
∵点P在圆O上,∴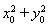 =5.
=5.
∴k1·k2=-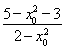 =-1.
=-1.
∴两条切线的斜率之积为常数-1


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题4练习卷(解析版) 题型:解答题
设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1.
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习真题感悟江苏专用常考问题1练习卷(解析版) 题型:填空题
将一个长宽分别是a,b(0<b<a)的铁皮的四角切去相同的正方形,然后折成一个无盖的长方体的盒子,若这个长方体的外接球的体积存在最小值,则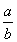 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测5练习卷(解析版) 题型:填空题
如图,正方体ABCD ?A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测5练习卷(解析版) 题型:填空题
盒子里共有大小相同的3只白球,1只黑球.若从中随机摸出两只球,则它们颜色相同的概率是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测4练习卷(解析版) 题型:填空题
设双曲线 -y2=1的右焦点为F,点P1、P2、…、Pn是其右上方一段(2≤x≤2
-y2=1的右焦点为F,点P1、P2、…、Pn是其右上方一段(2≤x≤2 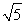 ,y≥0)上的点,线段|PkF|的长度为ak(k=1,2,3,…,n).若数列{an}成等差数列且公差d∈
,y≥0)上的点,线段|PkF|的长度为ak(k=1,2,3,…,n).若数列{an}成等差数列且公差d∈ ,则n的最大取值为________.
,则n的最大取值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测4练习卷(解析版) 题型:填空题
设圆C的圆心与双曲线 =1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线l:x-
=1(a>0)的右焦点重合,且该圆与此双曲线的渐近线相切,若直线l:x- y=0被圆C截得的弦长等于2,则a的值为________.
y=0被圆C截得的弦长等于2,则a的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测3练习卷(解析版) 题型:填空题
Sn是等比数列{an}的前n项和,a1= ,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为________.
,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测1练习卷(解析版) 题型:填空题
已知函数f(x)= x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.
x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com