
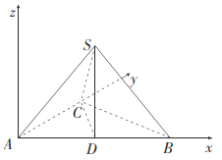
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析.
(2)![]() .
.
【解析】分析:(1)证![]() ,
,![]() .即可由线面垂的判定定理得出结论;
.即可由线面垂的判定定理得出结论;
(2)通过建系,分别求出面DSC和面SCA的法向量![]() ,进行计算,观察图中二面角的范围得出余弦值的符号
,进行计算,观察图中二面角的范围得出余弦值的符号
(1)证明:因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() .
.
因为![]() ,且
,且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解:如图,建立空间直角坐标系![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
易得![]() ,
,![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
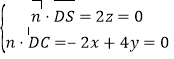 ,取
,取![]() ,则
,则![]() ,
,![]() ,
,
所以![]() .
.
又因为![]() 为平面
为平面![]() 的一个法向量,所以
的一个法向量,所以![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
点晴:空间立体是高考必考的解答题之一,在做这类题目时,正面题大家需要注意书写的步骤分,判定定理的必要点必须要有;另外在求角等问题时我们可以利用向量法进行解决问题,注意角的范围问题。


科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中, ![]() ,E,F分别是底边AB,CD的中点,把四边形BEFC沿直线EF折起,使得面BEFC⊥面ADFE,若动点P∈平面ADFE,设PB,PC与平面ADFE所成的角分别为θ1 , θ2(θ1 , θ2均不为0).若θ1=θ2 , 则动点P的轨迹为( )
,E,F分别是底边AB,CD的中点,把四边形BEFC沿直线EF折起,使得面BEFC⊥面ADFE,若动点P∈平面ADFE,设PB,PC与平面ADFE所成的角分别为θ1 , θ2(θ1 , θ2均不为0).若θ1=θ2 , 则动点P的轨迹为( ) 
A.直线
B.椭圆
C.圆
D.抛物线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在
在![]() 处的切线与
处的切线与![]() 在
在![]() 处的切线平行,求实数
处的切线平行,求实数![]() 的值;
的值;
(2)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(3)在(2)的条件下,若![]() ,求证:函数
,求证:函数![]() 只有一个零点
只有一个零点![]() ,且
,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.

(1)求该几何体的体积![]() ;
;
(2)求该几何体的表面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() .
.
(1)求过点![]() 且与圆
且与圆![]() 相切的直线
相切的直线![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)![]() 是圆
是圆![]() 上一动点,
上一动点,![]() ,若点
,若点![]() 为
为![]() 的中点,求动点
的中点,求动点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com