
| A. | 函数f(x)=x2(x∈R)存在1级“理想区间” | |
| B. | 函数f(x)=ex(x∈R)不存在2级“理想区间” | |
| C. | 函数f(x)=$\frac{4x}{{x}^{2}+1}$(x≥0)存在3级“理想区间” | |
| D. | 函数f(x)=tanx,x∈(-$\frac{π}{2}$,$\frac{π}{2}$)不存在4级“理想区间” |
分析 A、B、C中,可以找出定义域中的“理想区间”,从而作出正确的选择.D中,假设存在“理想区间”[a,b],会得出错误的结论.
解答 解:A中,当x≥0时,f(x)=x2在[0,1]上是单调增函数,且f(x)在[0,1]上的值域是[0,1],
∴存在1级“理想区间”,原命题正确;
B中,当x∈R时,f(x)=ex在[a,b]上是单调增函数,且f(x)在[a,b]上的值域是[ea,eb],
∴不存在2级“理想区间”,原命题正确;
C中,因为f(x)=$\frac{4x}{{x}^{2}+1}$=$\frac{4}{x+\frac{1}{x}}$在(0,1)上为增函数.
假设存在[a,b]?(0,1),使得f(x)∈[3a,3b]则有$\left\{\begin{array}{l}f(a)=3a\\ f(b)=3b\end{array}\right.$,所以命题正确;
D中,若函数(a>0,a≠1).不妨设a>1,则函数在定义域内为单调增函数,
若存在“4级理想区间”[m,n],
则由m,n是方程tanx=4x,x∈(-$\frac{π}{2}$,$\frac{π}{2}$)的两个根,
由于该方程不存在两个不等的根,
故不存在“4级理想区间”[m,n],
∴D结论错误
故选:D
点评 本题考查了新定义下的函数的性质与应用问题,解题时应理解新定义中的题意与要求,转化为解题的条件与结论,是易错题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
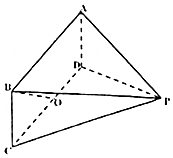 如图,已知四边形ABCD是矩形,AB=2BC=2,三角形PCD是正三角形,且平面ABCD⊥平面PCD.
如图,已知四边形ABCD是矩形,AB=2BC=2,三角形PCD是正三角形,且平面ABCD⊥平面PCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com