
分析 将直线方程代入圆的方程,△<0,求得b<$\sqrt{2}$a,利用古典概型概率公式,即可求得概率为P=1-$\frac{1}{3}$=$\frac{2}{3}$,
解答 解:$\left\{\begin{array}{l}{(x-3)^{2}+{y}^{2}=3}\\{ax+by=0}\end{array}\right.$,消去y,得$\frac{{a}^{2}+{b}^{2}}{{b}^{2}}$x2-6x+6=0,
若圆与直线无公共点,则△=(-6)2-4×6×$\frac{{a}^{2}+{b}^{2}}{{b}^{2}}$<0,化简得b<$\sqrt{2}$a;
(x,y)共有36种组合;满足b>$\sqrt{2}$a;条件的组合有(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,5),(3,6),(4,6),共有12种,
∴满足b>$\sqrt{2}$a的概率为$\frac{12}{36}$=$\frac{1}{3}$,
∴该古典概型的概率为P=1-$\frac{1}{3}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查直线与圆的位置关系,考查古典概型概率公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b1b2…bn=b1b2…b17-n (n<17,n∈N*) | |
| B. | b1b2…bn=b1b2…b18-n(n<18,n∈N*) | |
| C. | b1+b2+…+bn=b1+b2+…+b17-n(n<17,n∈N*) | |
| D. | b1+b2+…+bn=b1+b2-1+…+b18-n(n<18,n∈N*) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
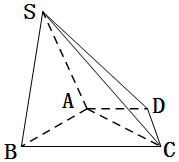 如图,如图,在四棱锥S-ABCD中,底面梯形ABCD中,BC∥AD,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2DC=2\sqrt{5}$.
如图,如图,在四棱锥S-ABCD中,底面梯形ABCD中,BC∥AD,平面SAB⊥平面ABCD,△SAB是等边三角形,已知$AC=2AB=4,BC=2AD=2DC=2\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)=x2(x∈R)存在1级“理想区间” | |
| B. | 函数f(x)=ex(x∈R)不存在2级“理想区间” | |
| C. | 函数f(x)=$\frac{4x}{{x}^{2}+1}$(x≥0)存在3级“理想区间” | |
| D. | 函数f(x)=tanx,x∈(-$\frac{π}{2}$,$\frac{π}{2}$)不存在4级“理想区间” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
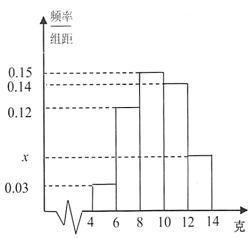 “累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801-2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:| 累积净化量(克) | (3,5] | (5,8] | (8,12] | 12以上 |
| 等级 | P1 | P2 | P3 | P4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com