
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 对各个选项分别加以判断:对①和②举出反例可得它们不正确;结合空间直线与平面、平面与平面平行和垂直的判定和性质,对③和④加以论证可得它们是真命题.
解答 解:对于①,若α⊥β,β⊥γ,则α∥γ或α,γ相交,故①不正确;
对于②,若l上两个点A、B满足线段AB的中点在平面内,则A、B到α的距离相等,但l与α相交,故②不正确;
对于③,若l⊥α,l∥β,则根据面面垂直的判定定理可知α⊥β,故③正确;
对于④,若α∥β且l∥α,可得l∥β或l在β内,而条件中有l?β,所以必定l∥β,故④正确.
故选D.
点评 本题以命题真假的判断为载体,着重考查了直线与平面、平面与平面平行的判定和性质,以及直线与平面、平面与平面垂直的判定和性质等知识,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{3}{5}$ | C. | -3 | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=4sin(2x+\frac{π}{6})$ | B. | $y=-2sin(2x+\frac{π}{6})+2$ | C. | $y=-2sin(x+\frac{π}{3})+2$ | D. | $y=2sin(2x+\frac{π}{3})+2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
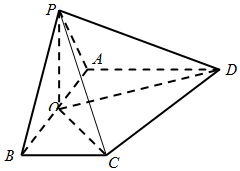 如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3
如图,已知在四棱锥P-ABCD中,O为AB中点,平面POC⊥平面ABCD,AD∥BC,AB⊥BC,PA=PB=BC=AB=2,AD=3查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b1b2…bn=b1b2…b17-n (n<17,n∈N*) | |
| B. | b1b2…bn=b1b2…b18-n(n<18,n∈N*) | |
| C. | b1+b2+…+bn=b1+b2+…+b17-n(n<17,n∈N*) | |
| D. | b1+b2+…+bn=b1+b2-1+…+b18-n(n<18,n∈N*) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)=x2(x∈R)存在1级“理想区间” | |
| B. | 函数f(x)=ex(x∈R)不存在2级“理想区间” | |
| C. | 函数f(x)=$\frac{4x}{{x}^{2}+1}$(x≥0)存在3级“理想区间” | |
| D. | 函数f(x)=tanx,x∈(-$\frac{π}{2}$,$\frac{π}{2}$)不存在4级“理想区间” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com