
 已知函数f(x)=2sin2($\frac{π}{4}$x+$\frac{π}{4}$)
已知函数f(x)=2sin2($\frac{π}{4}$x+$\frac{π}{4}$)分析 (Ⅰ)利用倍角公式和诱导公式对函数解析式进行化简,再利用正弦函数的五个关键点进行列表、描点、连线;
(Ⅱ)根据函数解析式先求出周期,再求出一个周期内的函数值的和,进而判断出2012与周期的关系,再求出式子和的值.
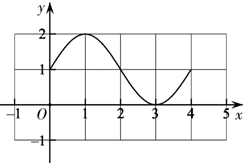
解答 解:(Ⅰ)$f(x)=2{sin^2}(\frac{π}{4}x+\frac{π}{4})=1-cos(\frac{π}{2}x+\frac{π}{2})=1+sin\frac{π}{2}x$.…4 分
列表得:
| x | 0 | 1 | 2 | 3 | 4 |
| $\frac{π}{2}x$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| $y=1+sin\frac{π}{2}x$ | 1 | 2 | 1 | 0 | 1 |
点评 本题是关于三角函数的综合题,涉及了倍角公式、诱导公式的应用,“五点作图法”的步骤,函数周期性的应用求式子的值,考查了分析、解决问题能力和作图能力.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com