
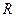 上的函数
上的函数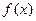 同时满足下列三个条件:
同时满足下列三个条件: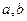 均有
均有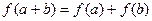 成立;
成立;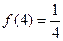 ;
;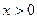 时,都有
时,都有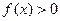 成立。
成立。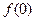 ,
, 的值;
的值;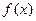 为
为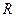 上的增函数
上的增函数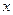 的不等式
的不等式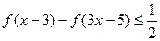 .
. 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源:不详 题型:解答题
 知每投放质量为
知每投放质量为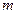 的药剂后,经过
的药剂后,经过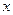 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度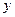 (毫克/升) 满足
(毫克/升) 满足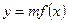 ,其中
,其中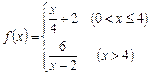 ,当药剂在水中释放的浓度不低于
,当药剂在水中释放的浓度不低于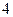 (毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于
(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于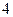 (毫克/升) 且不高于10(毫克/升)时称为最佳净化。
(毫克/升) 且不高于10(毫克/升)时称为最佳净化。 ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天? ,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量 的值。
的值。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.先增后减 | B.先减后增 |
| C.单调递增 | D.单调递减 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com