分析:(1)由题设知b=c,又a=2
,所以b=c=2,从而可得椭圆方程;
(2)设直线l的方程与椭圆方程联立,利用向量的数量积,结合韦达定理,即可求得直线l在y轴上的截距.
解答:(1)解:由题设知b=c,又a=2
,所以b=c=2,故椭圆方程为
+=1;…(2分)
(2)证明:因为M(0,2),所以直线l与x轴不垂直.
设直线l的方程为y=kx+m,A(x
1,y
1),B(x
2,y
2)
由
得(2k
2+1)x
2+4kmx+2m
2-8=0,所以x
1+x
2=-
,x
1x
2=
…(6分)
又
•=0,所以(x
1,y
1-2)•(x
2,y
2-2)=0,即x
1x
2+y
1y
2-2(y
1+y
2)+4=0,
x
1x
2+(kx
1+m)(kx
2+m)-2(kx
1+m+kx
2+m)+4=0,
整理得(k
2+1)x
1x
2+k(m-2)(x
1+x
2)+(m-2)
2=0,
即(k
2+1)×
+k(m-2)×(-
)+(m-2)
2=0,…(10分)
因为m≠2,所以2(k
2+1)(m+2)-4k
2m+(2k
2+1)(m-2)=0
展开整理得3m+2=0,即m=-
.
直线l在y轴上的截距为定值-
.…(12分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识,考查韦达定理的运用,综合性强.



 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案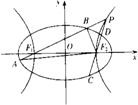 如图,已知椭圆E:
如图,已知椭圆E: