
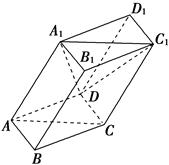
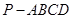 中,底面是以
中,底面是以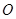 为中心的菱形,
为中心的菱形,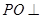 底面
底面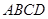 ,
,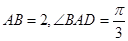 ,
,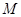 为
为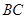 上一点,且
上一点,且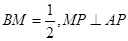 .
.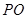 的长;
的长;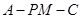 的正弦值.
的正弦值.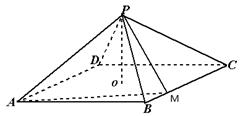
 ;(2)
;(2)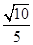 .
.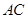 、
、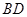 ,因为是菱形
,因为是菱形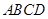 的中心,
的中心,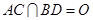 ,以
,以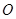 为坐标原点,
为坐标原点,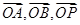 的方向分别为
的方向分别为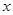 轴、
轴、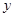 轴、
轴、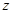 轴的正方向,建立空间直角坐标系,根据题设条件写出
轴的正方向,建立空间直角坐标系,根据题设条件写出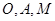 的坐标,并设出点
的坐标,并设出点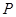 的坐标
的坐标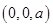 ,根据空间两点间的距离公式和勾股定理列方程解出
,根据空间两点间的距离公式和勾股定理列方程解出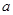 的值得到
的值得到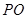 的长;.
的长;.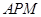 的法向量为
的法向量为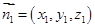 ,平面PMC的法向量为
,平面PMC的法向量为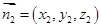 ,首先利用向量的数量积列方程求出向量
,首先利用向量的数量积列方程求出向量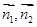 的坐标,再利用向量的夹角公式求出
的坐标,再利用向量的夹角公式求出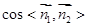 ,进而求出二面角
,进而求出二面角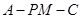 的正弦值.
的正弦值.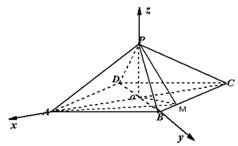
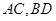 ,因
,因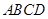 为菱形,则
为菱形,则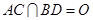 ,且
,且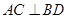 ,以
,以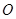 为坐标原点,
为坐标原点,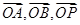 的方向分别为
的方向分别为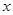 轴,
轴,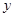 轴,
轴,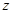 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系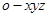 ,
,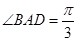 ,故
,故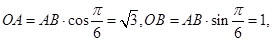
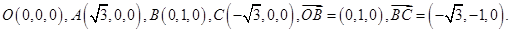
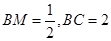 知,
知,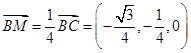
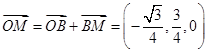 ,即
,即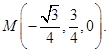
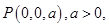 ,则
,则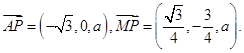 因为
因为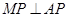 ,
,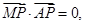 即
即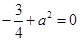 ,所以
,所以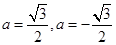 (舍去),即
(舍去),即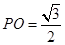 .
.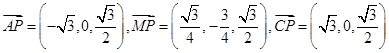 ,
,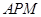 的法向量为
的法向量为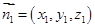 ,平面
,平面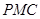 的法向量为
的法向量为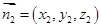
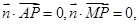 得
得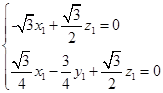 故可取
故可取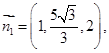
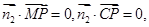 得
得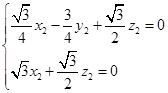 故可取
故可取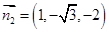
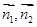 的夹角的余弦值为
的夹角的余弦值为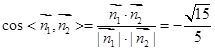
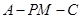 的正弦值为
的正弦值为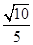 .
.

 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.平行 | B.相交 |
| C.异面垂直 | D.异面不垂直 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
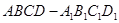 中,
中,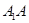
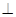 底面
底面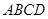 .四边形
.四边形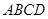 为梯形,
为梯形,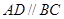 ,且
,且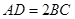 .过
.过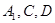 三点的平面记为
三点的平面记为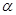 ,
,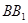 与
与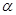 的交点为
的交点为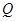 .
.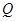 为
为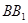 的中点;
的中点;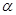 所分成上下两部分的体积之比;
所分成上下两部分的体积之比;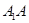
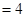 ,
,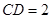 ,梯形
,梯形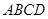 的面积为6,求平面
的面积为6,求平面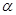 与底面
与底面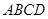 所成二面角大小.
所成二面角大小.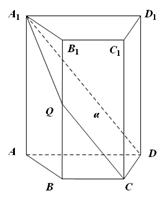
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com