
【题目】某项运动组委会为了搞好接待工作,招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余人不喜爱运动.得到下表:
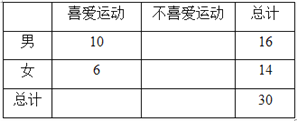
(1)根据以上数据完成2×2列联表, 问:能否在犯错误的概率不超过0.10的前提下,认为性别与喜爱运动有关?并说明理由.
(2)如果从喜欢运动的女志愿者中(其中恰有4人会外语)抽取2名,求抽出的志愿者中能胜任翻译工作的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: 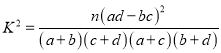
参考数据:

 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() :
: ![]() 上,而
上,而![]() 为
为![]() 在
在![]() 轴上的投影,且点
轴上的投影,且点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 是曲线
是曲线![]() 上两点,且
上两点,且![]() ,
, ![]() 为坐标原点,求
为坐标原点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,
, ![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的面积为
的面积为![]() ,椭圆
,椭圆![]() 的离心力为
的离心力为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知![]() 为坐标原点,直线
为坐标原点,直线![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
, ![]() 两个不同的点,若存在实数
两个不同的点,若存在实数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一条对称轴为
的一条对称轴为![]() ,且最高点的纵坐标是
,且最高点的纵坐标是![]() .
.
(1)求![]() 的最小值及此时函数
的最小值及此时函数![]() 的最小正周期、初相;
的最小正周期、初相;
(2)在(1)的情况下,设![]() ,求函数
,求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
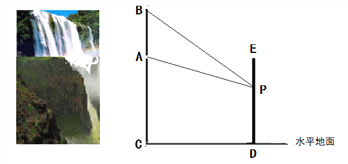
【题目】南京市江北新区计划在一个竖直长度为20米的瀑布![]() 正前方修建一座观光电梯
正前方修建一座观光电梯![]() 。如图所示,瀑布底部
。如图所示,瀑布底部![]() 距离水平地面的高度
距离水平地面的高度![]() 为60米,电梯上设有一个安全拍照口
为60米,电梯上设有一个安全拍照口![]() ,
, ![]() 上升的最大高度为60米。设
上升的最大高度为60米。设![]() 距离水平地面的高度为
距离水平地面的高度为![]() 米,
米, ![]() 处拍照瀑布的视角
处拍照瀑布的视角![]() 为
为![]() 。摄影爱好者发现,要使照片清晰,视角
。摄影爱好者发现,要使照片清晰,视角![]() 不能小于
不能小于![]() 。
。
(1)当![]() 米时,视角
米时,视角![]() 恰好为
恰好为![]() ,求电梯和山脚的水平距离
,求电梯和山脚的水平距离![]() 。
。
(2)要使电梯拍照口![]() 的高度
的高度![]() 在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离
在52米及以上时,拍出的照片均清晰,请求出电梯和山脚的水平距离![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() 为参数). 点
为参数). 点![]() 是曲线
是曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com