
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.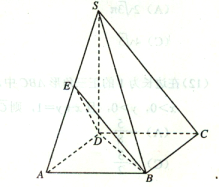
【答案】(1)详见解析(2)![]() .
.
【解析】
解:
(Ⅰ)∵SD⊥平面ABCD,∴平面SAD⊥平面ABCD,
∵AB⊥AD,∴AB⊥平面SAD,∴DE⊥AB.
∵SD=AD,E是SA的中点,∴DE⊥SA,
∵AB∩SA=A,∴DE⊥平面SAB
∴平面BED⊥平面SAB. …4分
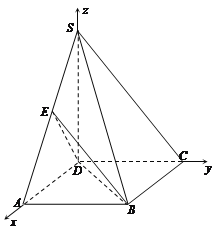
(Ⅱ)建立如图所示的坐标系D—xyz,不妨设AD=2,则
D(0,0,0),A(2,0,0),B(2,![]() ,0),
,0),
C(0,![]() ,0),S(0,0,2),E(1,0,1).
,0),S(0,0,2),E(1,0,1).
![]() =(2,
=(2,![]() ,0),
,0),![]() =(1,0,1),
=(1,0,1),![]() =(2,0,0),
=(2,0,0),![]() =(0,-
=(0,-![]() ,2).
,2).
设m=(x1,y1,z1)是面BED的一个法向量,则 因此可取m=(-1,
因此可取m=(-1,![]() ,1). …8分
,1). …8分
设n=(x2,y2,z2)是面SBC的一个法向量,则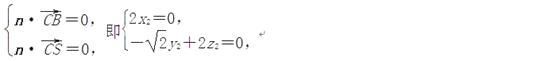 因此可取n=(0,
因此可取n=(0,![]() ,1). …10分
,1). …10分
 故平面BED与平面SBC所成锐二面角的大小为30°.…12分
故平面BED与平面SBC所成锐二面角的大小为30°.…12分


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,底面
中,底面![]() 是以
是以![]() 为斜边的等腰直角三角形,侧面
为斜边的等腰直角三角形,侧面![]() 是菱形且与底面
是菱形且与底面![]() 垂直,
垂直,![]() ,点
,点![]() 是
是![]() 中点,点
中点,点![]() 是
是![]() 上靠近
上靠近![]() 点的三等分点.
点的三等分点.
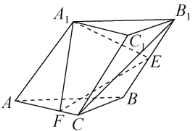
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
(2)试估计该市市民正确书写汉字的个数的众数与中位数;
(3)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市同组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,前n项和为
,前n项和为![]() ,对任意的正整数n,都有
,对任意的正整数n,都有![]() 恒成立.
恒成立.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知关于n的不等式![]() …
…![]() 对一切
对一切![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)已知 ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小并证明.
的大小并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
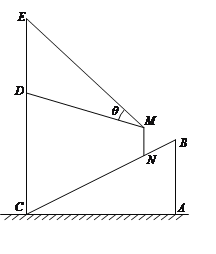
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高![]() 为
为![]() 米,它所占水平地面的长
米,它所占水平地面的长![]() 为
为![]() 米.该广告画最高点
米.该广告画最高点![]() 到地面的距离为
到地面的距离为![]() 米,最低点
米,最低点![]() 到地面距离
到地面距离![]() 米.假设某人眼睛到脚底的距离
米.假设某人眼睛到脚底的距离![]() 为
为![]() 米,他竖直站在此电梯上观看
米,他竖直站在此电梯上观看![]() 视角为
视角为![]() .
.
(Ⅰ)设此人到直线![]() 的距离为
的距离为![]() 米,试用含
米,试用含![]() 的表达式表示
的表达式表示![]() ;
;
(Ⅱ)此人到直线![]() 的距离为多少米时,视角
的距离为多少米时,视角![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com