考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)求导,令导数等于零,解方程,跟据f′(x)f(x)随x的变化情况即可求出函数的单调区间;
(2)假设存在a,使得k=2-a,根据(1)利用韦达定理求出直线斜率为k,根据(1)函数的单调性,推出矛盾,即可解决问题.
解答:
解解:(1)f(x)定义域为(0,+∞),
f′(x)=1+
-=
,
令g(x)=x
2-ax+1,△=a
2-4,
①当-2≤a≤2时,△≤0,f′(x)≥0,故f(x)在(0,+∞)上单调递增,
②当a<-2时,△>0,g(x)=0的两根都小于零,在(0,+∞)上,f′(x)>0,故f(x)在(0,+∞)上单调递增,
③当a>2时,△>0,g(x)=0的两根为x
1=
,x
2=
,
当0<x<x
1时,f′(x)>0;当x
1<x<x
2时,f′(x)<0;当x>x
2时,f′(x)>0;
故f(x)分别在(0,
),(
,+∞)上单调递增,在(
,
)上单调递减.
(2)由(I)知,a>2.
因为f(x
1)-f(x
2)=(x
1-x
2)+
-a(lnx
1-lnx
2),
所以k═1+(
=1+
-a•
,
又由(1)知,x
1x
2=1.于是
k=2-a•
,
若存在a,使得k=2-a,则
=1,即lnx
1-lnx
2=x
1-x
2,
亦即 x
2-
-2lnx
2=0,(x
2>1)(*)
再由(1)知,函数h(t)=t-
-2lnt在(0,+∞)上单调递增,
而x
2>1,
所以x
2-
-2lnx
2>1-1-2ln1=0,这与(*)式矛盾,
故不存在a,使得k=2-a.
点评:本题考查利用导数研究函数的单调性和极值问题,对方程f'(x)=0有无实根,有实根时,根是否在定义域内和根大小进行讨论,体现了分类讨论的思想方法,其中问题(2)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.属于难题.



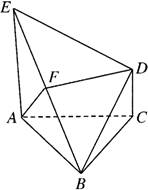 已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;
已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;