
分析 (1)当0<x≤10时,$P=xf(x)-(10+2.7x)=8.1x-\frac{x^3}{30}-10$,当x>10时,$P=xf(x)-(10+2.7x)=98-\frac{1000}{3x}-2.7x$,由此能求出年利润P(万元)关于该特许商品x(千件)的函数解析式.
(2)当0<x≤10时,由P′=0,得x=9,推导出当x=9时,P取最大值,且Pmax=38.6;当x>10时,P≤38.由此得到当年产量为9千件时,该公司在该特许商品生产中获利最大.
解答 解:(1)当0<x≤10时,$P=xf(x)-(10+2.7x)=8.1x-\frac{x^3}{30}-10$
当x>10时,$P=xf(x)-(10+2.7x)=98-\frac{1000}{3x}-2.7x$,
∴P=$\left\{\begin{array}{l}{8.1x-\frac{{x}^{3}}{30}-10,0<x≤10}\\{98-\frac{1000}{3x}-2.7x,x>10}\end{array}\right.$;(6分)
(2)(Ⅱ)①当0<x≤10时,
由P′=8.1-$\frac{{x}^{2}}{10}$=0,得x=9,且当x∈(0,9)时,P′>0,
当x∈(9,10)时,P′<0.
∴当x=9时,P取最大值,且Pmax=8.1×9-$\frac{1}{30}×93$-10=38.6.…(9分)
②当x>10时,P=98-($\frac{1000}{3x}+2.7x$)<38,
当且仅当$\frac{1000}{3x}=2.7x$,即x=$\frac{100}{9}$时,Pmax=38.
综合①、②知x=9时,P取最大值.…(11分)
所以当年产量为9千件时,该公司在该特许商品生产中获利最大.…(12分)
点评 本题考查函数的解析式的求法,考查年利润的最大值的求法.解时要认真审题,注意分类讨论思想和等价转化思想的合理运用.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
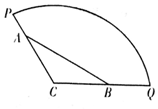 为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长$60\sqrt{3}$米.
为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长$60\sqrt{3}$米.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)>1,则$\frac{b+1}{a+1}$的取值范围是( )
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)>1,则$\frac{b+1}{a+1}$的取值范围是( )| A. | ($\frac{1}{5}$,$\frac{1}{3}$) | B. | (-∞,3) | C. | (-∞,$\frac{1}{3}$) | D. | ($\frac{1}{3}$,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
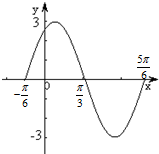 已知函数y=Asin(ωx+φ)(A>0,ω>0)|φ|<$\frac{π}{2}$的图象如图所示,
已知函数y=Asin(ωx+φ)(A>0,ω>0)|φ|<$\frac{π}{2}$的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
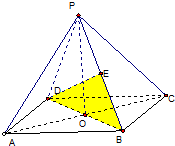 如图正方形ABCD中,O为中心,PO⊥面ABCD,E是PC中点,求证:
如图正方形ABCD中,O为中心,PO⊥面ABCD,E是PC中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{24}$ | B. | x=$\frac{5π}{12}$ | C. | x=$\frac{π}{2}$ | D. | x=$\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com