
 Ϊ�����������й۹⣬�������ƻ��ڰ뾶Ϊ200�ף�Բ�Ľ�Ϊ120������ι㳡�ڣ���ͼ��ʾ�����ء�ABC�߽����۹��·������A��B�ֱ����߶�CP��CQ�ϣ���A��B��������Ϊ����$60\sqrt{3}$�ף�
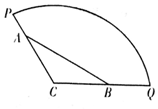
Ϊ�����������й۹⣬�������ƻ��ڰ뾶Ϊ200�ף�Բ�Ľ�Ϊ120������ι㳡�ڣ���ͼ��ʾ�����ء�ABC�߽����۹��·������A��B�ֱ����߶�CP��CQ�ϣ���A��B��������Ϊ����$60\sqrt{3}$�ף����� ��1������֪�����Ҷ������ɵý�BC��ֵ��
��2����CA=x��CB=y��x��y�ʣ�0��200]���������Ҷ�������${��60\sqrt{3}��^2}={x^2}+{y^2}+xy$����ϻ�������ʽ����x+y��120���Ӷ�����۹��·�ܳ����ֵ��
��� �⣺��1���ڡ�ABC�У�����֪�����Ҷ�����$\frac{AB}{sin��ACB}=\frac{BC}{sin��BAC}$��
��$\frac{{60\sqrt{3}}}{{sin{{120}��}}}=\frac{BC}{{sin{{45}��}}}$��
��$BC=60\sqrt{2}m$��
��2����CA=x��CB=y��x��y�ʣ�0��200]��
�ڡ�ABC�У�AB2=AC2+CB2-2AC•CB•cos120�㣬��${��60\sqrt{3}��^2}={x^2}+{y^2}+xy$��
��${��60\sqrt{3}��^2}={��x+y��^2}-xy��{��x+y��^2}-\frac{{{{��x+y��}^2}}}{4}=\frac{3}{4}{��x+y��^2}$��
��x+y��120�����ҽ���x=y=60ʱ��x+yȡ�����ֵ��
�൱A��B�������C��60�״�ʱ���۹��·�ܳ��ȴﵽ����Ϊ$��120+60\sqrt{3}��m$��
���� ������Ҫ���������Ҷ��������Ҷ�������������ʽ�ڽ��������е�Ӧ�ã������˼���������ת��˼�룬�����е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��+�ޣ� | B�� | [0��2] | C�� | [1��2] | D�� | ��-�ޣ�2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{n}{3��2n+3��}$ | B�� | $\frac{2n}{3��2n+3��}$ | C�� | $\frac{n-1}{3��2n+1��}$ | D�� | $\frac{n}{2n+1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�11�� | B�� | ��1��11] | C�� | ��1��11�� | D�� | ��1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 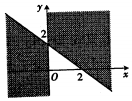 | B�� | 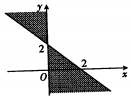 | C�� |  | D�� | 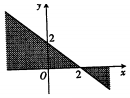 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com