
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | a<c<b | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
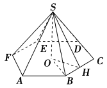 正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.
正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,30) | [30,45) | [45,60) | [60,75) |
| 人数 | 24 | 26 | 16 | 14 |
| 赞成人数 | 12 | 14 | x | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
| A. | 9400 | B. | 9408 | C. | 9410 | D. | 9414 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
| g(x) | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
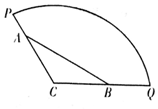 为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长$60\sqrt{3}$米.
为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长$60\sqrt{3}$米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com