
| A. | (-∞,11) | B. | (1,11] | C. | (1,11) | D. | (1,+∞) |
科目:高中数学 来源: 题型:解答题
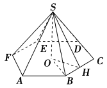 正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.
正六棱锥得底面周长为24,O是底面的中心,H是BC的中点,∠SHO=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -4 | C. | -5 | D. | $-\frac{15}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
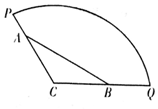 为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长$60\sqrt{3}$米.
为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长$60\sqrt{3}$米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10π | B. | 22π | C. | 24π | D. | 28π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)>1,则$\frac{b+1}{a+1}$的取值范围是( )
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)>1,则$\frac{b+1}{a+1}$的取值范围是( )| A. | ($\frac{1}{5}$,$\frac{1}{3}$) | B. | (-∞,3) | C. | (-∞,$\frac{1}{3}$) | D. | ($\frac{1}{3}$,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com