
【题目】已知函数![]() .
.
(1)若![]() 是
是![]() 的极值点,求
的极值点,求![]() 的极大值;
的极大值;
(2)求实数![]() 的范围,使得
的范围,使得![]() 恒成立.
恒成立.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)先对函数求导,结合极值存在的条件可求t,然后结合导数可研究函数的单调性,进而可求极大值;
(2)由已知代入可得,x2+(t﹣2)x﹣tlnx≥0在x>0时恒成立,构造函数g(x)=x2+(t﹣2)x﹣tlnx,结合导数及函数的性质可求.
(1)![]() ,x>0,
,x>0,
由题意可得,![]() 0,解可得t=﹣4,
0,解可得t=﹣4,
∴![]() ,
,
易得,当x>2,0<x<1时,f′(x)>0,函数单调递增,当1<x<2时,f′(x)<0,函数单调递减,
故当x=1时,函数取得极大值f(1)=﹣3;
(2)由f(x)=x2+(t﹣2)x﹣tlnx+2≥2在x>0时恒成立可得,x2+(t﹣2)x﹣tlnx≥0在x>0时恒成立,
令g(x)=x2+(t﹣2)x﹣tlnx,则![]() ,
,
(i)当t≥0时,g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
所以g(x)min=g(1)=t﹣1≥0,解可得t≥1,
(ii)当﹣2<t<0时,g(x)在(![]() )上单调递减,在(0,
)上单调递减,在(0,![]() ),(1,+∞)上单调递增,
),(1,+∞)上单调递增,
此时g(1)=t﹣1<﹣1不合题意,舍去;
(iii)当t=﹣2时,g′(x)![]() 0,即g(x)在(0,+∞)上单调递增,此时g(1)=﹣3不合题意;
0,即g(x)在(0,+∞)上单调递增,此时g(1)=﹣3不合题意;
(iv)当t<﹣2时,g(x)在(1,![]() )上单调递减,在(0,1),(
)上单调递减,在(0,1),(![]() )上单调递增,此时g(1)=t﹣1<﹣3不合题意,
)上单调递增,此时g(1)=t﹣1<﹣3不合题意,
综上,t≥1时,f(x)≥2恒成立.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线的参数方程为
中,直线的参数方程为 (
(![]() 为参数).以原点为极点,轴正半轴为极轴建立极坐标系,曲线极坐标方程为
为参数).以原点为极点,轴正半轴为极轴建立极坐标系,曲线极坐标方程为![]() ,直线与曲线交于、两点.
,直线与曲线交于、两点.
(1)求直线的普通方程以及曲线的直角坐标方程;
(2)若直线上有定点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=C1C=1,M,N分别是AB,A1C的中点.

(1)求证:直线MN⊥平面ACB1;
(2)求点C1到平面B1MC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
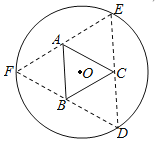
【题目】如图,圆形纸片的圆心为![]() ,半径为
,半径为![]() ,该纸片上的等边三角形
,该纸片上的等边三角形![]() 的中心为
的中心为![]() .
.![]() ,
,![]() ,
,![]() 为圆
为圆![]() 上的点,
上的点,![]() 分别是以
分别是以![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() 为折痕折起
为折痕折起![]() ,使得
,使得![]() ,
,![]() ,
,![]() 重合,得到三棱锥.当所得三棱锥体积(单位:
重合,得到三棱锥.当所得三棱锥体积(单位:![]() )最大时,
)最大时,![]() 的边长为_________(
的边长为_________(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求![]() 的值;
的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com