
【题目】已知函数![]() 在点
在点![]() 处的切线斜率为0.函数
处的切线斜率为0.函数![]()
(1)试用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)求![]() 的单调区间;
的单调区间;
(3)令![]() ,设函数
,设函数![]() 在
在![]()
![]() 处取得极值,记点
处取得极值,记点![]() ,
,![]() ,证明:线段
,证明:线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() ,
,![]() 的公共点.
的公共点.
【答案】(1)![]() .(2)答案见解析.(3)证明见解析
.(2)答案见解析.(3)证明见解析
【解析】
(1)求导后利用![]() ,即可得解;
,即可得解;
(2)求导后分![]() ,
,![]() 和
和![]() 三种情况讨论求出单调区间即可;
三种情况讨论求出单调区间即可;
(3)由![]() 的极值得到
的极值得到![]() ,
,![]() 两点的坐标,进一步得到直线
两点的坐标,进一步得到直线![]() 的方程,联立方程求解即可得解.
的方程,联立方程求解即可得解.
(1)由![]() ,得
,得![]() ,
,
∵![]() 在点
在点![]() 处的切线斜率为0,
处的切线斜率为0,
∴![]() ,∴
,∴![]() ;
;
(2)由(1)得![]() ,则
,则
![]() ,
,
令![]() ,则
,则![]() 或
或![]() ,
,
①当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,
此时![]() 在
在![]() 和
和![]() 上单调递增;
上单调递增;
②当![]() 时,
时,![]() ,此时
,此时![]() 恒成立,且仅有
恒成立,且仅有![]() 时
时![]() ,
,
∴![]() 在
在![]() 上单调递增;
上单调递增;
③当![]() 时,
时,![]() ,
,
同理可得![]() 的增区间为
的增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ;
;
综上,当![]() 时,
时,![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() 和
和![]() ;当
;当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ;当
;当![]() 时,
时,![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() 和
和![]() ;
;
(3)当![]() 时,
时,![]() ,
,
令![]() ,则
,则![]() 或
或![]() ,
,
由(2)得![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ,
,
∴函数![]() 在
在![]() 和3处取得极值,
和3处取得极值,
∴![]() ,
,![]() ,所以
,所以 .
.
∴直线![]() 的方程为
的方程为![]() ,
,
由 得
得![]() ,
,
令![]() ,
,
易得![]() ,
,![]() ,
,
而![]() 的图象在(0,2)内是一条连续不断的曲线,
的图象在(0,2)内是一条连续不断的曲线,
故![]() 在(0,2)内存在零点
在(0,2)内存在零点![]() ,即线段
,即线段![]() 与曲线
与曲线![]() 有异于
有异于![]() ,
,![]() 的公共点.
的公共点.


科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面的问题中,并解决该问题.
这三个条件中任选一个,补充在下面的问题中,并解决该问题.
已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ______________,
______________,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个不同平面![]() 、
、![]() 、
、![]() 和直线
和直线![]() ,下面有四个命题:
,下面有四个命题:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②直线![]() 上有两点到平面
上有两点到平面![]() 的距离相等,则
的距离相等,则![]() ;
;
③![]() ,
,![]() ,则
,则![]() ;
;
④若直线![]() 不在平面
不在平面![]() 内,
内,![]() ,
,![]() ,则
,则![]() .
.
则正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改编自中国神话故事的动画电影《哪吒之魔童降世》自7月26日首映,在不到一个月的时间,票房收入就超过了38亿元,创造了中国动画电影的神话.小明和同学相约去电影院观看《哪吒之魔童降世》,影院的三个放映厅分别在7:30,8:00,8:30开始放映,小明和同学大约在7:40至8:30之间到达影院,且他们到达影院的时间是随机的,那么他们到达后等待的时间不超过10分钟的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双十一购物狂欢节,是指每年11月11日的网络促销日,源于淘宝商城(天猫)2009年11月11日举办的网络促销活动,已成为中国电子商务行业的年度盛事.某生产商为了了解其生产的产品在不同电商平台的销售情况,统计了![]() 两个电商平台各十个网络销售店铺的销售数据:
两个电商平台各十个网络销售店铺的销售数据:
| 64 | 71 | 81 | 70 | 79 | 69 | 82 | 73 | 75 | 60 |
| 60 | 80 | 97 | 77 | 96 | 87 | 76 | 83 | 94 | 96 |
(1)作出![]() 两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
两个电商平台销售数据的茎叶图,根据茎叶图判断哪个电商平台的销售更好,并说明理由;
(2)填写下面关于店铺个数的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 的把握认为销售量与电商平台有关;
的把握认为销售量与电商平台有关;
销售量 | 销售量 | 总计 | |
| |||
| |||
总计 |
(3)生产商要从这20个网络销售店铺销售量前五名的店铺中,随机抽取三个店铺进行销售返利,则其中恰好有两个店铺的销售量在95以上的概率是多少?
附: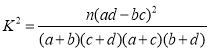 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
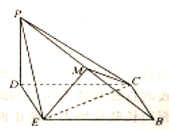
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,离心率
,离心率![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,圆
为原点,圆![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一动点,若直线
上一动点,若直线![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com