
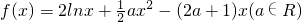 .
. 时,求函数f(x)在[1,e]上的最大值和最小值;
时,求函数f(x)在[1,e]上的最大值和最小值; 时,f′(x)=-
时,f′(x)=- ,….(2分)
,….(2分)| x | [1,2) | 2 | (2,e] |
| f′(x) | + | 0 | - |
| f(x) | 增 | 2ln2-1 | 减 |
 ,f(e)=2-
,f(e)=2- ,….(5分)
,….(5分) .….(7分)
.….(7分) ,….(8分)
,….(8分) 时,由f′(x)>0得0<x<2或x>
时,由f′(x)>0得0<x<2或x> ,
, ,+∞),
,+∞), ,
, ); ….(10分)
); ….(10分) 时,f′(x)≥0在(0,+∞)上恒成立,且当且仅当f′(2)=0,
时,f′(x)≥0在(0,+∞)上恒成立,且当且仅当f′(2)=0, 时,由f′(x)>0得0<x<
时,由f′(x)>0得0<x< 或x>2,
或x>2, ),(2,+∞),
),(2,+∞), <x<2,
<x<2, ,2).….(13分)
,2).….(13分) 时,可求得f′(x),令f′(x)=0,可求得极值点,将x的取值情况,f′(x)正负情况及f(x)的增减情况列表,可求得函数f(x)在[1,e]上的最大值和最小值;
时,可求得f′(x),令f′(x)=0,可求得极值点,将x的取值情况,f′(x)正负情况及f(x)的增减情况列表,可求得函数f(x)在[1,e]上的最大值和最小值; =
=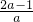 ,对0<a<
,对0<a< ,a=
,a= 及a>
及a> 时分类讨论,根据f′(x)的正负情况即可得到函数的单调区间.
时分类讨论,根据f′(x)的正负情况即可得到函数的单调区间.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com