
如图,边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点△AED,△EBF,△FCD分别沿DE,EF,FD折起,使A,B,C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为

A. B.
B. C.
C. D.
D.
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源:2014年高考数学三轮冲刺模拟 概率与统计(解析版) 题型:解答题
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
品牌 | 甲 |
|
| 乙 |
|
首次出现故障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
每辆利润(万元) | 1 | 2 | 3 | 1.8 | 2.9 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率;
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列;
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量(解析版) 题型:解答题
已知函数f(x)= cos
cos ,x∈R.
,x∈R.
(1)求f 的值;
的值;
(2)若cos θ= ,θ∈
,θ∈ ,求f
,求f .
.
查看答案和解析>>
科目:高中数学 来源:2014年吉林省延边州高考复习质量检测理科数学试卷(解析版) 题型:填空题
.给出下列命题:
① 已知线性回归方程 ,当变量
,当变量 增加2个单位,其预报值平均增加4个单位;
增加2个单位,其预报值平均增加4个单位;
② 在进制计算中, ;
;
③ 若 ,且
,且 ,则
,则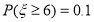 ;
;
④ “ ”是“函数
”是“函数 的最小正周期为4”的充要条件;
的最小正周期为4”的充要条件;
⑤ 设函数 的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
查看答案和解析>>
科目:高中数学 来源:2014年吉林省延边州高考复习质量检测文科数学试卷(解析版) 题型:解答题
如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5。

求:(1)⊙O的半径;
(2)s1n∠BAP的值。
查看答案和解析>>
科目:高中数学 来源:2014年吉林省延边州高考复习质量检测文科数学试卷(解析版) 题型:选择题
 表示不同直线,M表示平面,给出四个命题:①若
表示不同直线,M表示平面,给出四个命题:①若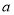 ∥M,
∥M, ∥M,则
∥M,则 ∥
∥ 或
或 相交或
相交或 异面;②若
异面;②若 M,
M, ∥
∥ ,则
,则 ∥M;③
∥M;③ ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ∥
∥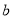 ;④
;④ ⊥M,
⊥M, ⊥M,则
⊥M,则 ∥
∥ ,其中正确命题为
,其中正确命题为
A.①④ B.②③ C.③④ D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com