练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，PA为⊙O的切线，A为切点，PBC是过点O的割线，PA=10，PB=5。

    求：（1）⊙O的半径；

    （2）s1n∠BAP的值。

     

    （1）7.5（2）

    【解析】

    试题分析：（1）由题可知，利用切割线定理即可；（2）根据弦切角定理可知s1n∠BAP=s1n∠ACB，然后求出AB、BC的比值即可.

    试题解析：（1）因为PA为⊙O的切线，所以,

    又由PA=10，PB=5，所以PC=20，BC=20-5=15 2分.

    因为BC为⊙O的直径，所以⊙O的半径为7.5. 4分

    （2）∵PA为⊙O的切线，∴∠ACB=∠PAB, 5分

    又由∠P=∠P, ∴△PAB∽△PCA,∴ 7分

    设AB=k，AC=2k, ∵BC为⊙O的直径，

    ∴AB⊥AC∴ 8分

    ∴s1n∠BAP=s1n∠ACB= 10分

    考点：平面几何中圆的性质.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 概率与统计（解析版） 题型：选择题

    执行两次如图所示的程序框图，若第一次输入的a的值为－1．2，第二次输入的a的值为1．2，则第一次，第二次输出的a的值分别为( )

    A．0．2,0．2 B．0．2,0．8

    C．0．8,0．2 D．0．8,0．8

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量（解析版） 题型：选择题

    在△ABC中，若sin2A＋sin2B＜sin2C，则△ABC的形状是(　　)

    A．锐角三角形 B．直角三角形

    C．钝角三角形 D．不能确定

     

    查看答案和解析>>

    科目：高中数学 来源：2014年吉林省延边州高考复习质量检测理科数学试卷（解析版） 题型：选择题

    如图，边长为2的正方形ABCD中，点E，F分别是边AB，BC的中点△AED，△EBF，△FCD分别沿DE，EF，FD折起，使A，B，C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上，则该球的半径为

    A． B． C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年吉林省延边州高考复习质量检测理科数学试卷（解析版） 题型：选择题

    “”是“”的

    A．必要不充分条件 B．充分不必要条件

    C．充要条件 D．既不充分也不必要条件

     

    查看答案和解析>>

    科目：高中数学 来源：2014年吉林省延边州高考复习质量检测文科数学试卷（解析版） 题型：解答题

    已知数列是公差不为0的等差数列，a1=2且a2,a3,a4＋1成等比数列。

    (1)求数列的通项公式；

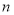    （2）设，求数列的前项和

     

    查看答案和解析>>

    科目：高中数学 来源：2014年吉林省延边州高考复习质量检测文科数学试卷（解析版） 题型：选择题

    已知正数a,b满足4a＋b=30，使得取最小值的实数对(a,b)是

    A．(5，10） B．(6，6) C．(10，5) D．(7，2)

     

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年浙江省嘉兴市高二暑假作业检测数学试卷（解析版） 题型：填空题

    已知，那么的最小值是.

     

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年江西省高二上学期开学考试数学试卷（解析版） 题型：解答题

    已知向量，，，．

    （1）求与的夹角；

    （2）若，求实数的值．

     

    查看答案和解析>>

    同步练习册答案