
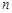 个红球(
个红球( 且
且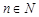 )和
)和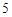 个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。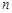 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率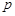 ;
;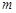 ,求
,求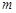 的最大值.
的最大值.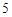 个白球全部取出后,对剩下的
个白球全部取出后,对剩下的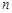 个红球全部作如下标记:记上
个红球全部作如下标记:记上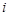 号的有
号的有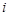 个(
个(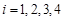 ),其余的红球记上
),其余的红球记上 号,现从袋中任取一球。
号,现从袋中任取一球。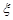 表示所取球的标号,求
表示所取球的标号,求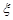 的分布列、期望和方差.
的分布列、期望和方差.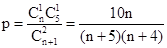 ;(2)n=20时,m的最大值为4/9;
;(2)n=20时,m的最大值为4/9;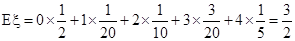 ,
,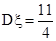 .
.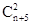 种方法。它们是等可能的,其中两个球的颜色不同的方法有
种方法。它们是等可能的,其中两个球的颜色不同的方法有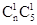 种,故一次摸奖中奖的概率为
种,故一次摸奖中奖的概率为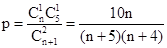 .
.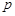 ,三次摸奖中恰有一次中奖的概率是:
,三次摸奖中恰有一次中奖的概率是: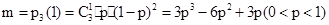 利用导数的思想求解最值。
利用导数的思想求解最值。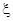 的可能取值为0,1,2,3,4求解各个概率值,然后求解期望和方差即可。
的可能取值为0,1,2,3,4求解各个概率值,然后求解期望和方差即可。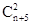 种方法。
种方法。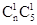 种,
种,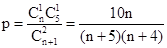 . ………5分
. ………5分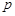 ,三次摸奖中恰有一次中奖的概率是:
,三次摸奖中恰有一次中奖的概率是: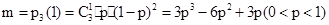 ……… 6分
……… 6分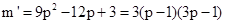
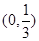 上为增函数,m在
上为增函数,m在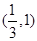 上为减函数。 ………8分
上为减函数。 ………8分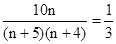 ,n=20时,m的最大值为4/9. ……… 10分
,n=20时,m的最大值为4/9. ……… 10分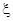 的分布列是:
的分布列是: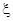 |  | 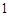 | 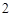 | 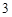 | 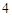 |
| p | 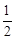 | 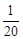 | 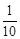 | 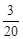 | 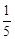 |
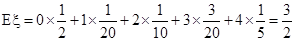 . ………14分
. ………14分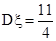 .……..15分
.……..15分

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个学分;考核为优秀,授予
个学分;考核为优秀,授予 个学分.假设该校志愿者甲、乙考核为优秀的概率分别为
个学分.假设该校志愿者甲、乙考核为优秀的概率分别为 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为 .甲、乙、丙三人考核所得等次相互独立.
.甲、乙、丙三人考核所得等次相互独立. ,求随机变量
,求随机变量 的
的查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
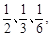 现对三只小白鼠注射这种药物.
现对三只小白鼠注射这种药物.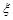 表示三只小白鼠共表现症状的种数,求
表示三只小白鼠共表现症状的种数,求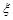 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
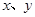 ,记
,记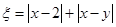 .
.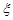 的最大值,并求事件“
的最大值,并求事件“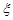 取得最大值”的概率;
取得最大值”的概率;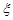 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com