
是否存在常数a,b,c使得等式1•22+2•32+…+n(n+1)2=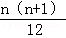 (an2+bn+c)对于一切正整数n都成立?并证明你的结论.
(an2+bn+c)对于一切正整数n都成立?并证明你的结论.
见解析
【解析】
试题分析:先假设存在符合题意的常数a,b,c,再令n=1,n=2,n=3构造三个方程求出a,b,c,再用用数学归纳法证明成立,证明时先证:(1)当n=1时成立.(2)再假设n=k(k≥1)时,成立,即1•22+2•32+…+k(k+1)2=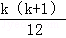 (3k2+11k+10),再递推到n=k+1时,成立即可.
(3k2+11k+10),再递推到n=k+1时,成立即可.
证明:假设存在符合题意的常数a,b,c,
在等式1•22+2•32+…+n(n+1)2
=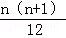 (an2+bn+c)中,
(an2+bn+c)中,
令n=1,得4= (a+b+c)①
(a+b+c)①
令n=2,得22=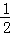 (4a+2b+c)②
(4a+2b+c)②
令n=3,得70=9a+3b+c③
由①②③解得a=3,b=11,c=10,
于是,对于n=1,2,3都有
1•22+2•32+…+n(n+1)2=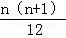 (3n2+11n+10)(*)成立.
(3n2+11n+10)(*)成立.
下面用数学归纳法证明:对于一切正整数n,(*)式都成立.
(1)当n=1时,由上述知,(*)成立.
(2)假设n=k(k≥1)时,(*)成立,
即1•22+2•32+…+k(k+1)2
=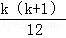 (3k2+11k+10),
(3k2+11k+10),
那么当n=k+1时,
1•22+2•32+…+k(k+1)2+(k+1)(k+2)2
=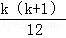 (3k2+11k+10)+(k+1)(k+2)2
(3k2+11k+10)+(k+1)(k+2)2
=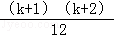 (3k2+5k+12k+24)
(3k2+5k+12k+24)
=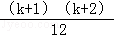 [3(k+1)2+11(k+1)+10],
[3(k+1)2+11(k+1)+10],
由此可知,当n=k+1时,(*)式也成立.
综上所述,当a=3,b=11,c=10时题设的等式对于一切正整数n都成立.


科目:高中数学 来源:[同步]2015年北师大版选修1-1 3.3计算导数练习卷(解析版) 题型:选择题
下列运算正确的是( )
A.(ax2﹣bx+c)′=a(x2)′+b(﹣x)′
B.(sinx﹣2x2)′=(sinx)′﹣(2)′(x2)′
C.(cosxsinx)′=(sinx)′cosx+(cosx)′cosx
D.[(3+x2)(2﹣x3)]′=2x(2﹣x3)+3x2(3+x2)
查看答案和解析>>
科目:高中数学 来源:[同步]2015年北师大版必修一 3.1 正整数指数函数练习卷(解析版) 题型:填空题
已知不等式(a2+a+2)2x>(a2+a+2)x+8,其中x∈N+,使此不等式成立的x的最小整数值是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2015年北师大版必修一 2.1 生活中的变量关系练习卷(解析版) 题型:填空题
给出下列关系:
①人的年龄与他(她)拥有的财富之间的关系;
②抛物线上的点与该点坐标之间的关系;
③橘子的产量与气候之间的关系;
④某同学在6次考试中的数学成绩与他的考试号之间的关系.
其中不是函数关系的有 .
查看答案和解析>>
科目:高中数学 来源:[同步]2015年北师大版必修一 2.1 生活中的变量关系练习卷(解析版) 题型:选择题
如图,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面上升高度h与注水时间t之间的函数关系,大致是( )
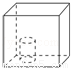
A.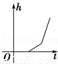 B.
B.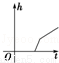 C.
C.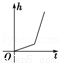 D.
D.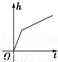
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版选修4-5 3.1 数学归纳法原理练习卷(解析版) 题型:选择题
用数学归纳法证明1+r+r2+…+rn=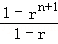 (n∈N,r≠1),在验证n=0时,左端计算所得项为( )
(n∈N,r≠1),在验证n=0时,左端计算所得项为( )
A.1 B.r C.1+r D.1+r+r2
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教B版必修二2.4 空间直角坐标系练习卷(解析版) 题型:解答题
在空间直角坐标系中,已知A(3,0,1)和B(1,0,﹣3),试问
(1)在y轴上是否存在点M,满足|MA|=|MB|?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标.
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教A版选修1-1 3.4生活中的优化问题举例练习卷(解析版) 题型:填空题
横梁的强度和它的矩形横断面的宽成正比,并和矩形横断面的高的平方成正比,要将直径为d的圆木锯成强度最大的横梁,则横断面的宽是 .
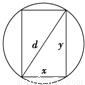
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com