Question

9．已知f（x）=|2^x-1|．
（1）求f（x）的单调区间；
（2）比较f（x+1）与f（x）的大小；
（3）试确定函数g（x）=f（x）-x²零点的个数．

Answer 1

分析 （1）将函数转化为分段函数，利用分段函数确定函数单调区间．
（2）利用函数的单调性比较大小．
（3）转化函数的零点与函数的图象的交点，画出函数的图象，判断即可．

解答 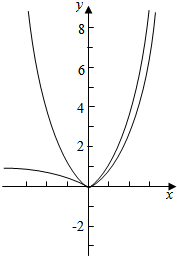解：（1）当x≥0时，函数f（x）=|2^x-1|=2^x-1，此时函数单调递增．
当x＜0时，函数f（x）=|2^x-1|=-（2^x-1）=1-2^x，此时函数单调递减．
∴函数的单调递增区间为[0，+∞），单调递减为（-∞，0）．
（2）若x≥0，则x+1≥1，此时函数f（x）单调递增，∴f（x+1）＞f（x），
若x+1≤0，则x≤-1，此时函数f（x）单调递递减，∴f（x+1）＜f（x），
若x+1＞0且x＜0，即-1＜x＜0时，
f（x）=-2^x+1，f（x+1）=|2^x+1-1|=2^x+1-1，
则f（x+1）-f（x）=2^x+1-1-（1-2^x）=2^x+2^x+1-2=3?2^x+1-2＞0，
∴f（x+1）＞f（x），
综上：当x≤-1时，f（x）＜f（x+1）．
当x＞-1时，f（x）＞f（x+1）．
（3）由（1）可知函数f（x）=|2^x-1|在x=0时取得最小值0，
g（x）=f（x）-x²=0，
即|2^x-1|=x²，在坐标系中画出函数y=|2^x-1|与y=x²的图象，如图：
两个函数的图象的交点有3个．
函数g（x）=f（x）-x²零点的个数为3．

点评 本题主要考查了指数函数的单调性的应用，以及利用作差法比较大小．函数的零点个数的判断，考查数形结合以及运算能力，分类讨论思想的应用．