练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．执行如图所示的程序框图，如果输入的N是5，那么输出的p是（　　）
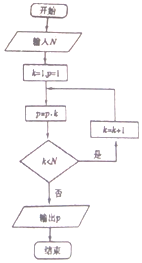
    A．120B．720C．1440D．5040

    分析 由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量p的值，模拟程序的运行过程，可得答案．

    解答 解：模拟程序的运行，可得：
    第一次执行循环体后，p=1，满足继续循环的条件k＜N（k＜5），则k=2
    再次执行循环体后，p=2，满足继续循环的条件k＜N（k＜5），则k=3，
    执行循环体后，p=6，满足继续循环的条件k＜N（k＜5），则k=4，
    执行循环体后，p=24，满足继续循环的条件k＜N（k＜5），则k=5，
    执行循环体后，p=120，不满足继续循环的条件k＜N（k＜5），
    故输出结果为：120，
    故选：A．

    点评 本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．如图，在矩形ABCD中，AB=3，BC=2，若点E为BC的中点，点F在CD上，$\overrightarrow{AB}$•$\overrightarrow{AF}$=6，则$\overrightarrow{AE}$•$\overrightarrow{BF}$的值为-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．四棱锥P-ABCD的底面与四个侧面的形状和大小如图所示．

    （1）写出四棱锥P-ABCD中四对线面垂直关系（不要求证明）；
    （2）在四棱锥P-ABCD中，若E为PA的中点，求证：BE∥平面PCD；
    （3）在四棱锥P-ABCD中，设面PAB与面PCD所成的角为θ（0°＜θ≤90°），求cosθ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．为调查了解某高等院校毕业生参加工作后，从事的工作与大学所学专业是否专业对口，该校随机调查了80位该校2015年毕业的大学生，得到具体数据如下表：
    专业对口专业不对口合计
    男301040
    女35540
    合计651580
    （1）能否在犯错误的概率不超过5%的前提下，认为“毕业生从事的工作与大学所学专业对口与性别有关”？
    参考公式：${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$（n=a+b+c+d）．
    附表：
    P（K）0.500.400.250.150.100.050.0250.010
     0.4550.7081.3232.0722.3063.8415.0216.635
    （2）求这80位毕业生从事的工作与大学所学专业对口的频率；
    （3）以（2）中的频率作为概率．该校近几年毕业的2000名大学生中随机选取4名，记这4名毕业生从事的工作与大学所学专业对口的人数为X，求X的数学期望E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设函数f（x）=$\frac{1}{3}a{x}^{3}+\frac{1}{2}b{x}_{2}+cx（a，b，c∈R，a≠0）$的图象在点（x，f（x））处的切线的斜率为k（x），且函数g（x）=k（x）-$\frac{1}{2}x$为偶函数．若函数k（x）满足下列条件：①k（-1）=0；②对一切实数x，不等式k（x）$≤\frac{1}{2}{x}^{2}+\frac{1}{2}$恒成立．
    （Ⅰ）求函数k（x）的表达式；
    （Ⅱ）设函数h（x）=lnx${\;}^{2}-（2m+3）x+\frac{12f（x）}{x}（x＞0）$的两个极值点x1，x2（x1＜x2）恰为φ（x）=lnx-sx2-tx的零点．当m$≥\frac{3\sqrt{2}}{2}$时，求y=（x1-x2）φ′（$\frac{{x}_{1}+{x}_{2}}{2}$）的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知等差数列{an}的公差为d，a3=5，且（a1x+d）5的展开式中x2与x3的系数之比为2：1．
    （1）求（a1x-a2）6的展开式中二项式系数最大的项；
    （2）设[a1x2-（a3-a1）x+a3]n=b0+b1（x-2）+b2（x-2）2+…+b2n（x-2）2n，n∈N*，求a1b1+a2b2+…+a2nb2n的值；
    （3）当n≥2时，求证：$（{a}_{n+1}）^{{a}_{n+1}}$＞11×16n+8n4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．若$|{\overrightarrow{AB}}|=18，|{\overrightarrow{AC}}|=5$，则$|{\overrightarrow{BC}}|$的取值范围是[13，23]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．若?x0∈[1，2]，使不等式${x_0}^2-m{x_0}+4＞0$成立，则m的取值范围是（-∞，5）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=$\left\{\begin{array}{l}{x^2}+a\;\;\;\;\;x≥0\\{2^x}\;\;\;\;\;\;\;\;\;\;x＜0\end{array}$，其中a∈R．
    （1）若a=0，解不等式f（x）≥$\frac{1}{4}$；
    （2）已知函数y=f（x）存在反函数，其反函数记为y=f-1（x）．若关于x的不等式：f-1（4-a）≤f（x）在x∈[0，+∞）上恒成立，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案