
分析 (1)根据等差数列的性质和二项式展开定理求出a1=1,d=2,即可求出展开式中二项式系数最大的项,
(2)根据二项式展开定理,得到b1=b3=b5=…=b2n-1=0,b0=Cn0,b2=Cn1,…b2n=Cnn,继而得到a1b1+a2b2+…+a2nb2n=3Cn1+7Cn2+11Cn3+…+(4n-1)Cnn,利用倒序相加法即可求出答案,
(3)根据二项式展开定理和多次放缩即可证明.
解答 解:(1)等差数列{an}的公差为d,a3=5,且(a1x+d)5的展开式中x2与x3的系数之比为2:1.
∴a1=5-2d且${C}_{5}^{3}({a}_{1})^{2}{d}^{3}=2{C}_{5}^{2}{(a}_{1})^{3}{d}^{2}$,
解得a1=1,d=2,
∴an=2n-1,
∴(a1x-a2)6=(x-3)6
∴(x-3)6的展开式中二项式系数最大的项是第四项为${C}_{6}^{3}{x}^{3}(-3)^{3}$=-540x3;
(2)∵a1=1,a3=5,则[a1x2-(a3-a1)x+a3]n=[(x-2)2+1]n=Cn0[(x-2)2]0+Cn1[(x-2)2]1+…+Cnn-1[(x-2)2]n-1+Cnn[(x-2)2]n,
=Cn0(x-2)2+Cn1(x-2)2+…+Cnn-1(x-2)2n-2+Cnn(x-2)2n,
=b0+b1(x-2)+b2(x-2)2+…+b2n(x-2)2n,n∈N*,
∴b1=b3=b5=…=b2n-1=0,b0=Cn0,b2=Cn1,…b2n=Cnn,
∴a1b1+a2b2+…+a2nb2n=3Cn1+7Cn2+11Cn3+…+(4n-1)Cnn,
令S=3Cn1+7Cn2+11Cn3+…+(4n-1)Cnn,
则S=[(-1)Cn0+3Cn1+Cn2+11Cn3+…+(4n-1)Cnn]+1
即S=[[(4n-1)Cnn+(4n-5)Cnn-1+…+(-1)Cn0]+1,
∴2S=(4n-2)(Cn0+Cn1+Cn2+Cn3+…+Cnn)+2
∴S=(2n-1)×2n+1;
(3):$({a}_{n+1})^{{a}_{n+1}}$=(2n+1)2n+1=(2n)2n+1+C2n1(2n)2n+C2n2(2n)2n-1+…+C2n2n-1(2n)2+1,
∵n>2,
∴2n>4,
∴$({a}_{n+1})^{{a}_{n+1}}$=(2n+1)2n+1>42n+1+C5142n+C5242n-1+C2n2(2n)2>4×16n+5×16n+$\frac{5}{2}$×16n+8n4>11×16n+8n4.
点评 本题考查了二项式展开定理和等差数列的性质,以及倒序相加法和放缩法,运算量大,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
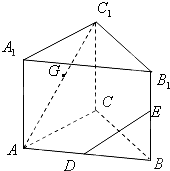 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 4 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com