
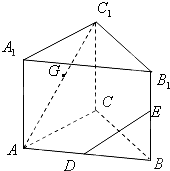
 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.分析 (1)棱B1C1上F,且F为B1C1的中点,连接AB1,则DE∥AB1∥GF.DE到平面AB1C1的距离是点B到直线AB1距离的一半,由此能示出结果.
(2)延长FE与CB的延长线交于M,连接DM,则DM为截面与底面所成二面角的棱,取BC的中点N,连FN,则FN∥BB1.作EH⊥DM于H,连BH,由三垂线定理可知∠EHB为截面与底面所成的锐二面角.由此能求出结果.
解答 解:(1)棱B1C1上F,且F为B1C1的中点,使GF∥DE.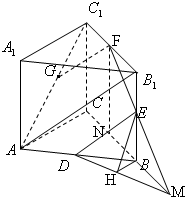
连接AB1,
∵D、E、G分别是AB1、BB1、AC1的中点,
∴DE∥AB1∥GF.
∵正三棱柱ABC-A1B1C1中,
D是AB的中点,E是BB1的中点,∴DE∥AB1,
∵AB=BB1=2,
∴DE到平面AB1C1的距离是点B到直线AB1距离的一半,
∴DE到平面AB1C1的距离d=$\frac{1}{2}\sqrt{4-1}$=$\frac{\sqrt{3}}{2}$.
(2)延长FE与CB的延长线交于M,连接DM,
则DM为截面与底面所成二面角的棱,
取BC的中点N,连FN,则FN∥BB1.
∵EB∥FN,EB=$\frac{1}{2}$FN,∴B为MN的中点.
由题设得BM=BN=BE=BD=1,且∠DEM=120°,
作EH⊥DM于H,则∠BDM=∠BMD=30°,连BH,
又BE⊥底面ABC,
由三垂线定理可知BH⊥DM,
∴∠EHB为截面与底面所成的锐二面角.
在Rt△EHB中,BE=1,EH=$\frac{1}{2}$BD=$\frac{1}{2}$,
∴tan∠EHB=$\frac{BE}{EH}$=2.
点评 本题考查线面垂直的点的位置的确定,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
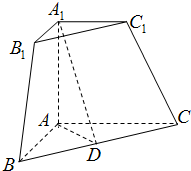 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=AC=2A1C1=2,D为BC中点.
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=$\sqrt{3}$,AB=AC=2A1C1=2,D为BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 专业对口 | 专业不对口 | 合计 | |
| 男 | 30 | 10 | 40 |
| 女 | 35 | 5 | 40 |
| 合计 | 65 | 15 | 80 |
| P(K) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.306 | 3.841 | 5.021 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com