
分析 A∩B={$\frac{1}{2}$},得到$\frac{1}{2}$∈A且$\frac{1}{2}$∈B,代入即可求得p,q的值,从而求得集合A,B,进而求得A∪B.
解答 解:A∩B={$\frac{1}{2}$},
∴$\frac{1}{2}$∈A且$\frac{1}{2}$∈B,
∴2×$\frac{1}{4}$+$\frac{3}{2}$p+2=0,2×$\frac{1}{4}$+$\frac{1}{2}$+q=0,
解得p=-$\frac{5}{3}$,q=-1,
∴A={$\frac{1}{2}$,2},B={-1,$\frac{1}{2}$},
∴A∪B={-1,$\frac{1}{2}$,2}
点评 此题是中档题.考查集合的交集的定义和一元二次方程的解法,体现了方程的思想和转化的思想,同时考查了运算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
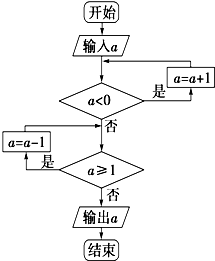 运行两次如图所示的程序框图,若第一次与第二次输入的a的值之和为0,则第一次与第二次输出的a的值之和为( )
运行两次如图所示的程序框图,若第一次与第二次输入的a的值之和为0,则第一次与第二次输出的a的值之和为( )| A. | 0 | B. | 1 | C. | 0或1 | D. | -1或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com