Question

1．在△ABC中，已知AC边上的中线BD=$\sqrt{5}$，E是BC边上的中点，DE=$\frac{2\sqrt{6}}{3}$，cosB=$\frac{\sqrt{6}}{6}$，求△ABC的三边长．

Answer 1

分析 由题意，AB=$\frac{4\sqrt{6}}{3}$．延长BD至E，使得DE=BD，连接CE，△BCE中，由余弦定理建立方程，求边长BC的值，再求出AC即可．

解答 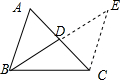解：由题意，AB=$\frac{4\sqrt{6}}{3}$．
延长BD至E，使得DE=BD，连接CE，则cos∠BCE=-$\frac{\sqrt{6}}{6}$，CE=$\frac{4\sqrt{6}}{3}$，BE=2$\sqrt{5}$，
△BCE中，由余弦定理可得20=（$\frac{4\sqrt{6}}{3}$）²+BC²-2×$\frac{4\sqrt{6}}{3}$×BC×（-$\frac{\sqrt{6}}{6}$），
∴BC²+$\frac{8}{3}$BC-$\frac{28}{3}$=0，
∴BC=2（负数舍去）．
∴AC²=（$\frac{4\sqrt{6}}{3}$）²+2²-2×$\frac{4\sqrt{6}}{3}$×2×（$\frac{\sqrt{6}}{6}$），
∴AC=$\frac{2\sqrt{21}}{3}$．

点评 本题考查余弦定理，考查学生的计算能力，考查学生分析解决问题的能力，属于中档题．