
在直角坐标系中,曲线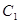 的参数方程为
的参数方程为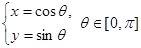 ,以
,以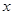 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线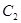 在极坐标系中的方程为
在极坐标系中的方程为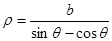 .若曲线
.若曲线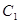 与
与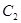 有两个不同的交点,则实数
有两个不同的交点,则实数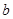 的取值范围是 .
的取值范围是 .
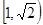
解析试题分析:因为曲线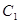 的参数方程为
的参数方程为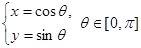 化成直角坐标方程为: x2+y2=1,图象是圆心在原点半径为1的上半圆.曲线C2利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得曲线C2在的直角坐标方程,在直角坐标方程方程是: x-y+b=0.由圆心到直线的距离得:d=
化成直角坐标方程为: x2+y2=1,图象是圆心在原点半径为1的上半圆.曲线C2利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得曲线C2在的直角坐标方程,在直角坐标方程方程是: x-y+b=0.由圆心到直线的距离得:d= =1,得到b=±
=1,得到b=±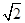
结合图象得:实数b的取值范围是1≤b<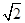
故答案为:1≤b<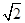
考点:本试题主要考查了点的极坐标和直角坐标的互化,圆的参数方程,体会数形结合的思想,能进行极坐标和直角坐标的互化.
点评:解决该试题的关键是先消去参数θ得到曲线的普通方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得曲线C2在的直角坐标方程.在直角坐标系中画出它们的图形,由图观察即可得实数b的取值范围。


科目:高中数学 来源: 题型:填空题
方程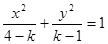 表示的曲线为
表示的曲线为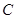 ,给出下列四个命题:
,给出下列四个命题:
①曲线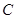 不可能是圆; ②若
不可能是圆; ②若 ,则曲线
,则曲线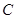 为椭圆;③若曲线
为椭圆;③若曲线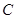 为双曲线,则
为双曲线,则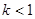 或
或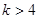 ;④若曲线
;④若曲线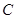 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则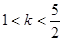 .
.
其中正确的命题是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com