
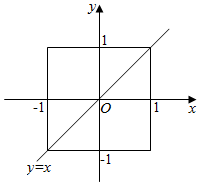 如图,平面直角坐标系内点P(x,y)的横坐标x与纵坐标y满足:-1≤x≤1,-1≤y≤1.
如图,平面直角坐标系内点P(x,y)的横坐标x与纵坐标y满足:-1≤x≤1,-1≤y≤1.分析 (1)符合古典概型,找到所有的基本事件,再找到满足条件的基本事件的个数,根据概率公式计算即可,
(2)符合几何概型,先求出正方形的面积,再求出满足条件的三角形的面积,根据概率公式计算即可.
解答 解:(1)x∈Z,y∈Z,则基本事件的个数为(1,1),(1,-1),(-1,1),(-1,1),(0,1),(0,-1),(1,0),(-1,0),(0,0)共9个,
其中满足点P(x,y)满足y=x为事件A为(1,1),(-1,-1),(0,0)共3个,
故事件A的概率P1=$\frac{3}{9}$=$\frac{1}{3}$,
(2)x∈R,y∈R,则基本事件的面积为边长为2的正方形的面积为2×2=4,
其中记点P(x,y)满足y≥x为事件B,其面积为正方形的面积的一半为2,
故事件B的概率P2=$\frac{1}{2}$.
点评 本题考查了古典概型和几何概型概率的问题,属于基础题.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 周期为3π的偶函数 | B. | 周期为2π的奇函数 | ||
| C. | 周期为3π的奇函数 | D. | 周期为$\frac{4π}{3}$的偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{m-1}}{m-1}$ | B. | $\frac{-2\sqrt{-m}}{m}$ | C. | $\frac{2\sqrt{m}}{m}$ | D. | -$\frac{2\sqrt{1-m}}{m-1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com