练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    为了倡导健康、低碳、绿色的生活理念，某市建立了公共自行车服务系统鼓励市民租用公共自行车出行，公共自行车按每车每次的租用时间进行收费，具体收费标准如下：

        ①租用时间不超过1小时，免费；

        ②租用时间为1小时以上且不超过2小时，收费1元；

        ③租用时间为2小时以上且不超过3小时，收费2元；

        ④租用时间超过3小时的时段，按每小时2元收费（不足1小时的部分按1小时计算）

        已知甲、乙两人独立出行，各租用公共自行车一次，两人租车时间都不会超过3小时，设甲、乙租用时间不超过1小时的概率分别是0.4和0.5 ，租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.

       （Ⅰ）求甲、乙两人所付租车费相同的概率；

    （Ⅱ）设甲、乙两人所付租车费之和为随机变量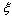，求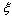的分布列和数学期望E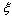

    0

    1

    2

    3

    4

    P

    0.2

    0.37

    0.28

    0.13

    0.02

    的数学期望,………………………11分

    答：甲、乙两人所付租车费相同的概率为0.37，的数学期望E=1.4.  …………12分

    考点：1、互斥事件、独立事件、和事件；2、离散型随机变量的分布列与数学期望.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知各项不为0的等差数列满足，数列是等比数列，且，则等于（     ）

    A．1   B．2   C．4   D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设等差数列{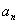 }的前n项和为Sn，且S4=4S2，．

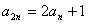    （1）求数列{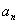}的通项公式；

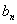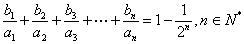    （2）设数列{ }满足，求{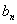}的前n项和Tn；

    （3）是否存在实数K，使得Tn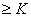恒成立.若有，求出K的最大值，若没有，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若为实数，则下列命题正确的是（  ）

    A．若，则                 B．若，则

    C．若，则                 D．若，则

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    点是不等式组表示的平面区域内的一动点，且不等式总成立，则的取值范围是________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆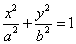(a>b>0)经过点M(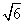，1)，离心率为．

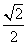    (1)求椭圆的标准方程；

    (2)已知点P(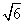，0)，若A，B为已知椭圆上两动点，且满足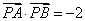，试问直线AB是否恒过定点，若恒过定点，请给出证明，并求出该定点的坐标；若不过，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数有(　　)

    A．极大值，极小值         B．极大值，极小值

    C．极大值，无极小值          D．极小值，无极大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    寒假期间，我市某校学生会组织部分同学，用“10分制”随机调查“阳光花园”社区人们的幸福度，现从调查人群中随机抽取16名，如果所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）；若幸福度分数不低于8.5分，则该人的幸福度为“幸福”.

    （I）求从这16人中随机选取3人，至少有2人为“幸福”的概率；

    （II）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记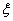表示抽到“幸福”的人数，求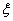的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a=3,b=log,c=log,则（）

    A.a>b>cB.b>c>aC.b>a>cD.c>b>a

    查看答案和解析>>

    同步练习册答案