
【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)设函数![]() ,若
,若![]() 有两个零点
有两个零点![]() .
.
(i)求![]() 的取值范围;
的取值范围;
(ii)证明:![]() .
.
【答案】(1)见解析;(2)(i)![]() ;(ii)证明见解析.
;(ii)证明见解析.
【解析】
(1)![]() ,分
,分![]() ,
,![]() ,
,![]() ,
,![]() 四种情况讨论即可;
四种情况讨论即可;
(2)(i)由(1)知![]() ,且
,且![]() 在
在![]() 处取得极大值
处取得极大值![]()
![]() ,当
,当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]() ,所以只需
,所以只需![]()
![]() ,构造函数解不等式即可;(ii)构造函数
,构造函数解不等式即可;(ii)构造函数![]() ,
,![]() ,利用导数结合
,利用导数结合![]() 的单调性证明即可.
的单调性证明即可.
(1)![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ;
;
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递增;
上单调递增;
③当![]() 时,
时,![]() ,
,![]() 或
或![]() ,
,
![]() ,∴
,∴![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
④当![]() 时,
时,![]() ,
,![]() 或
或![]() ,
,
![]() ,∴
,∴![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)![]() ,
,
![]()
(i)若![]() ,则
,则![]() 恒成立,
恒成立,![]() 在
在![]() 上递增,所以
上递增,所以![]() 至多一个零点,与已知不符合,故
至多一个零点,与已知不符合,故![]()
当![]() 时,
时,![]() ,
,![]()
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 处取得极大值,为
处取得极大值,为![]()
![]()
当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]()
∵![]() 有两个零点,所以只需极大值
有两个零点,所以只需极大值![]() ,即
,即![]()
设![]() ,
,
则![]() ,所以
,所以![]() 在
在![]() 上单调递减
上单调递减
又![]() ,所以使得
,所以使得![]() 的
的![]() .
.
(ii)结合(i)的分析,不妨设![]() ,
,
设![]() ,
,![]() ,
,
所以![]()
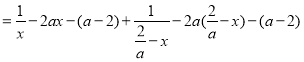
![]()
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
∵![]() ,且
,且![]() ,∴
,∴![]()
![]()
又![]() ,∴
,∴![]() ,
,
由![]() ,可知
,可知![]() 与
与![]() 均属于
均属于![]() ,
,
又![]() 在
在![]() 上单调递减,
上单调递减,
∴由![]() ,即
,即![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义域为
定义域为![]() ,部分对应值如表,
,部分对应值如表,![]() 的导函数
的导函数![]() 的图象如图所示. 下列关于函数
的图象如图所示. 下列关于函数![]() 的结论正确的有( )
的结论正确的有( )
|
|
|
|
|
|
|
|
|
|
|
|

A.函数![]() 的极大值点有
的极大值点有![]() 个
个
B.函数在![]() 上
上![]() 是减函数
是减函数
C.若![]() 时,
时,![]() 的最大值是
的最大值是![]() ,则
,则![]() 的最大值为4
的最大值为4
D.当![]() 时,函数
时,函数![]() 有
有![]() 个零点
个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上从春季进入夏季的标志为连续5天的日平均温度均不低于22℃.现有甲、乙、丙三地连续5天的日平均温度的记录数据:(记录数据都是正整数)
①甲地5个数据的中位数为24,众数为22;
②乙地5个数据的中位数为27,总体均值为24;
③丙地5个数据中有一个数据是32,总体均值为26,总体方差为10.8.
则肯定进入夏季的地区有_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示. 已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 .

(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中抽取教职工多少名?
(3)已知![]() ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知椭圆![]() :
:![]() 的左、右顶点分别为A,B,其离心率
的左、右顶点分别为A,B,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处取得极值,求实数
两处取得极值,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com