
分析 根据条件f(x0)≤f(x)≤f(x1+2016π)成立得到函数的最大值和最小值,结合三角函数的周期的性质建立不等式关系即可得到结论.
解答 解:函数f(x)=sin(ωx+φ)(ω>0),如果存在实数x0,
使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,
则f(x0)为函数的最小值,f(x0+2016π)为函数的最大值,
则x0+2016π-x0 =n•$\frac{T}{2}$=2016π,∵T=$\frac{2π}{ω}$,∴$\frac{1}{2}•\frac{2π}{ω}$=2016π,
即ω=$\frac{2nπ}{2016π}$×$\frac{1}{2}$=$\frac{n}{2016}$,∵n∈N•,∴当n=1时,ω=$\frac{1}{2016}$为最小值,
故答案为:$\frac{1}{2016}$.
点评 本题主要考查三角函数的图象和性质,根据函数的最值以及三角函数的周期公式是解决本题的关键,属于中档题.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:解答题
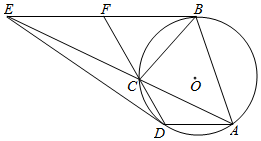 如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.
如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9日 | B. | 8日 | C. | 16日 | D. | 12日 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com