
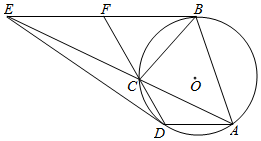
 如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.
如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.分析 (1)利用三角形的相似,结合切线长相等,即可证明:AB•CD=BC•AD;
(2)利用切割线定理,结合BF=EF,证明出△EFC∽△DFE,进而证明∠EFC=∠DAC,即可得出结论.
解答 证明:(1)∵过B、D两点的切线交于点E,
∴EB=ED,∠EBC=∠EAB,∠EDC=∠EAD
∵∠BEA=∠CEB,∠CED=∠DEA,
∴△EBC∽△EAB,△EDC∽△EAD,
∴$\frac{AB}{BC}=\frac{EA}{EB}$,$\frac{AD}{CD}=\frac{EA}{ED}$,
∴$\frac{AB}{BC}=\frac{AD}{CD}$,
∴AB•CD=BC•AD;
(2)∵BF2=FC•FD,BF=EF,
∴EF2=FC•FD,
∴$\frac{EF}{FC}=\frac{FD}{EF}$,
∵∠EFC=∠DFE,
∴△EFC∽△DFE,
∴∠FEC=∠FDE,
∵∠FDE=∠EAD,
∴∠EFC=∠DAC,
∴AD∥BE.
点评 本题考查圆的切线的性质,考查三角形相似的证明与性质的运用,证明三角形相似是关键.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
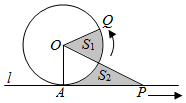 已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )
已知圆O与直线l相切于点A,点P,Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动,连接OQ,OP(如图),则阴影部分面积S1,S2的大小关系是( )| A. | S1=S2 | B. | S1≤S2 | ||
| C. | S1≥S2 | D. | 先S1<S2,再S1=S2,最后S1>S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | 1$+\frac{1}{2}$$+\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ | D. | 非以上答案 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com