
分析 (1)由函数的周期为π可得ω=2,再由对称中心为($\frac{π}{4}$,0)可得φ值,由函数图象变换和诱导公式可得;
(2)由三角函数的知识可得F(x)与原点距离最近的最大值和最小值点分别是点$(\frac{k}{2},\sqrt{3})$和$(-\frac{k}{2},-\sqrt{3})$,由题意结合图象可得${(\frac{k}{2})^2}+{(\sqrt{3})^2}≤{k^2}$,解不等式可得答案.
解答 解:(1)∵函数f(x)=sin(ωx+φ)的周期为π,ω>0,∴$ω=\frac{2π}{T}=2$,
又∵曲线y=f(x)的一个对称中心为($\frac{π}{4}$,0),φ∈(0,π),
∴sin(2×$\frac{π}{4}$+φ)=0,可得$φ=\frac{π}{2}$,∴f(x)=cos2x,
将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cosx的图象,
再将y=cosx的图象向右平移$\frac{π}{2}$个单位长度后得到函数g(x)=cos(x-$\frac{π}{2}$)的图象,
由诱导公式化简可得g(x)=sinx;
(2)∵函数y=F(x)=$\sqrt{3}sin\frac{πx}{k}$在$\frac{πx}{k}=nπ+\frac{π}{2}(n∈Z)$时取得最大值或最小值,
当$x=nk+\frac{k}{2}$,即与原点距离最近的最大值和最小值点分别是点$(\frac{k}{2},\sqrt{3})$和$(-\frac{k}{2},-\sqrt{3})$,
于是有${(\frac{k}{2})^2}+{(\sqrt{3})^2}≤{k^2}$,解不等式可得k≥2.
点评 本题考查三角函数图象变换,数形结合转化已知问题是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
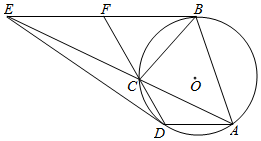 如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.
如图,圆O为四边形ABCD的外接圆,过B、D两点的切线交于点E,AE交圆O于点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com