
【题目】如图,在四边形ABCD中,| ![]() |=4,
|=4, ![]() =12,E为AC的中点.
=12,E为AC的中点. 
(1)若cos∠ABC= ![]() ,求△ABC的面积S△ABC;
,求△ABC的面积S△ABC;
(2)若 ![]() =2
=2 ![]() ,求
,求 ![]()
![]() 的值.
的值.
【答案】
(1)解:∵ ![]() ,∠ABC∈(0,π);
,∠ABC∈(0,π);
∴ ![]() ;
;
∵ ![]() =
= ![]() ;
;
∴ ![]() ;
;
∴ ![]() =
= ![]()
(2)解:以E为原点,AC所在直线为x轴,建立如图所示平面直角坐标系:
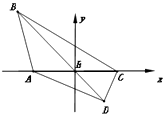
则A(﹣2,0),C(2,0),设D(x,y);
由 ![]() ,可得B(﹣2x,﹣2y);
,可得B(﹣2x,﹣2y);
则 ![]() =12;
=12;
∴x2+y2=4;
∴ ![]()
【解析】(1)容易求出sin∠ABC= ![]() ,并且可求出
,并且可求出 ![]() 的值,根据三角形面积公式即可求出△ABC的面积;(2)可以E为坐标原点,AC所在直线为x轴建立平面直角坐标系,并可得到A(﹣2,0),C(2,0),并设D(x,y),根据条件可求得E点坐标,从而求出
的值,根据三角形面积公式即可求出△ABC的面积;(2)可以E为坐标原点,AC所在直线为x轴建立平面直角坐标系,并可得到A(﹣2,0),C(2,0),并设D(x,y),根据条件可求得E点坐标,从而求出 ![]() 的坐标,进行数量积的坐标运算即可求得x2+y2=4,这样便可求出
的坐标,进行数量积的坐标运算即可求得x2+y2=4,这样便可求出 ![]() 的值.
的值.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣1|+|2x﹣3|,x∈R.
(1)若函数f(x)=|2x﹣1|+|2x﹣3|的最小值,并求取的最小值时x的取值范围;
(2)若g(x)= ![]() 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=blnx,g(x)=ax2﹣x(a∈R).
(1)若曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,求实数a、b的值;
(2)在(1)的条件下,证明f(x)≤g(x)在(0,+∞)上恒成立;
(3)若a=1,b>2e,求方程f(x)﹣g(x)=x在区间(1,eb)内实根的个数(e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知整数n≥4,集合M={1,2,3,…,n}的所有含有4个元素的子集记为A1 , A2 , A3 , …, ![]() .
.
设A1 , A2 , A3 , …, ![]() 中所有元素之和为Sn .
中所有元素之和为Sn .
(1)求S4 , S5 , S6并求出Sn;
(2)证明:S4+S5+…+Sn=10Cn+26 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是_____________.
①.如果命题“![]() ”与命题“
”与命题“![]() 或
或![]() ”都是真命题,那么命题
”都是真命题,那么命题![]() 一定是真命题.
一定是真命题.
②.命题![]() ,则
,则![]()
③.命题“若![]() ,则
,则![]() ”的否命题是:“若
”的否命题是:“若![]() ,则
,则![]() ”
”
④.特称命题 “![]() ,使
,使![]() ”是真命题.
”是真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() 是非零不共线的向量,设
是非零不共线的向量,设 ![]() =
= ![]()
![]() +
+ ![]()
![]() ,定义点集M={K|
,定义点集M={K| ![]() =
= ![]() },当K1 , K2∈M时,若对于任意的r≥2,不等式|
},当K1 , K2∈M时,若对于任意的r≥2,不等式| ![]() |≤c|
|≤c| ![]() |恒成立,则实数c的最小值为 .
|恒成立,则实数c的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学巨著,内容极为丰富,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”意思是:“5人分取5钱,各人所得钱数依次成等差数列,其中前2人所得钱数之和与后3人所得钱数之和相等.”,则其中分得钱数最多的是( )
A.![]() 钱
钱
B.1钱
C.![]() 钱
钱
D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面是以O为中心的菱形,
中,底面是以O为中心的菱形,![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,M为BC上一点.
,M为BC上一点.
![]() 当BM等于多少时,
当BM等于多少时,![]() 平面POM?
平面POM?
![]() 在满足
在满足![]() 的条件下,若
的条件下,若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图. (Ⅰ)这50个路段为中度拥堵的有多少个?
(Ⅱ)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望.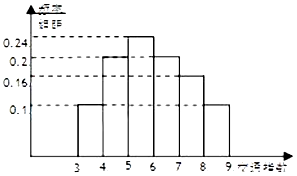
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com