在正三棱柱ABC—A1B1C1中，D是AC的中点，AB1⊥BC1，则平面DBC1与平面CBC1所成的角为( )
A．30° B．45° C．60° D．90°
一本好题口算题卡系列答案科目：高中数学 来源：2014年高考数学人教版评估检测 第七章 立体几何（解析版） 题型：填空题
等边三角形ABC与正方形ABDE有一公共边AB,二面角C-AB-D的余弦值为
,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于________.
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 解析几何（解析版） 题型：解答题
在平面直角坐标系xOy中，已知椭圆C的中心在原点O，焦点在x轴上，短轴长为2，离心率为
.
(1)求椭圆C的方程；
(2)设A，B是椭圆C上的两点，△AOB的面积为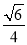
.若A、B两点关于x轴对称，E为线段AB的中点，射线OE交椭圆C于点P.如果
＝t
，求实数t的值．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：解答题
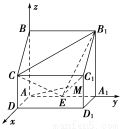
如图，四棱柱ABCD—A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD＝CD＝1，AA1＝AB＝2，E为棱AA1的中点．
(1)证明B1C1⊥CE；
(2)求二面角B1?CE?C1的正弦值；
(3)设点M在线段C1E上，且直线AM与平面ADD1A1所成角的正弦值为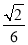
，求线段AM的长．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：填空题
对大于或等于2的自然数m的n次方幂有如下分解方式：
22＝1＋3 23＝3＋5
32＝1＋3＋5 33＝7＋9＋11
42＝1＋3＋5＋7 43＝13＋15＋17＋19
52＝1＋3＋5＋7＋9 53＝21＋23＋25＋27＋29
根据上述分解规律，若m3(m∈N*)的分解中最小的数是73，则m的值为________．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：选择题
点M、N分别是正方体ABCD—A1B1C1D1的棱A1B1、A1D1的中点，用过A、M、N和D、N、C1的两个截面截去正方体的两个角后得到的几何体如下图，则该几何体的正(主)视图、侧(左)视图、俯视图依次为( )
A．①②③ B．②③④
C．①③④ D．②④③
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 概率与统计（解析版） 题型：解答题
为备战2016年奥运会，甲、乙两位射击选手进行了强化训练．现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次，记录如下：
甲：8．3,9．0,7．9,7．8,9．4,8．9,8．4,8．3
乙：9．2,9．5,8．0,7．5,8．2,8．1,9．0,8．5
(1)画出甲、乙两位选手成绩的茎叶图；
(2)现要从中选派一人参加奥运会封闭集训，从统计学角度，你认为派哪位选手参加合理？简单说明理由；
(3)若将频率视为概率，对选手乙在今后的三次比赛成绩进行预测，记这三次成绩中不低于8．5分的次数为ξ，求ξ的分布列及均值E(ξ)．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 数列、推理与证明（解析版） 题型：解答题
(2013·杭州模拟)已知数列{an}的前n项和Sn＝－an－
n－1＋2(n∈N*)，数列{bn}满足bn＝2nan．
(1)求证数列{bn}是等差数列，并求数列{an}的通项公式．
(2)设数列
的前n项和为Tn，证明：n∈N*且n≥3时，Tn＞
．
(3)设数列{cn}满足an(cn－3n)＝(－1)n－1λn(λ为非零常数，n∈N*)，问是否存在整数λ，使得对任意n∈N*，都有cn＋1＞cn．
查看答案和解析>>
科目：高中数学 来源：2014年吉林省延边州高考复习质量检测理科数学试卷（解析版） 题型：解答题
如图，PA为⊙O的切线，A为切点，PBC是过点O的割线，PA=10，PB=5。
求：（1）⊙O的半径；
（2）s1n∠BAP的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
的方向分别为y轴和z轴的正方向建立空间直角坐标系．
a，a,0)，C1(0,2a,2b)，B1(
a，a,2b)．
⊥
，得
·
＝0，即2b2＝a2.
＝0，n1·
＝0.
又2b2＝a2，令z＝1，
，1)．
，0)．
＝
，得θ＝45°.
