
(2013·杭州模拟)已知数列{an}的前n项和Sn=-an- n-1+2(n∈N*),数列{bn}满足bn=2nan.
n-1+2(n∈N*),数列{bn}满足bn=2nan.
(1)求证数列{bn}是等差数列,并求数列{an}的通项公式.
(2)设数列 的前n项和为Tn,证明:n∈N*且n≥3时,Tn>
的前n项和为Tn,证明:n∈N*且n≥3时,Tn> .
.
(3)设数列{cn}满足an(cn-3n)=(-1)n-1λn(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有cn+1>cn.
(1)an=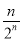 (n∈N*)
(n∈N*)
(2)见解析
(3)存在整数λ=-1,使得对任意n∈N*有cn+1>cn.
【解析】(1)在Sn=-an-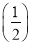 n-1+2中,令n=1,可得S1=-a1-1+2=a1,即a1=
n-1+2中,令n=1,可得S1=-a1-1+2=a1,即a1=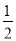 ,
,
当n≥2时,Sn-1=-an-1-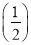 n-2+2,
n-2+2,
所以an=Sn-Sn-1=-an+an-1+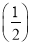 n-1,
n-1,
所以2an=an-1+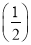 n-1,即2nan=2n-1an-1+1.
n-1,即2nan=2n-1an-1+1.
因为bn=2nan,所以bn=bn-1+1,即当n≥2时,bn-bn-1=1.
又b1=2a1=1,所以数列{bn}是首项和公差均为1的等差数列.
于是bn=1+(n-1)·1=n=2nan,
所以an=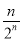 (n∈N*).
(n∈N*).
(2)由(1)得cn=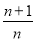 an=(n+1)
an=(n+1)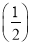 n,
n,
所以Tn=2×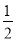 +3×
+3×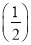 2+4×
2+4×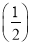 3+…+(n+1)
3+…+(n+1)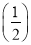 n,①
n,①
 Tn=2×
Tn=2× 2+3×
2+3×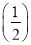 3+4×
3+4×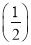 4+…+(n+1)
4+…+(n+1)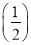 n+1.②
n+1.②
由①-②得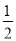 Tn=1+
Tn=1+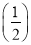 2+
2+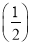 3+…+
3+…+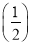 n-(n+1)
n-(n+1)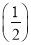 n+1
n+1
=1+ -(n+1)
-(n+1)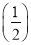 n+1
n+1
=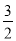 -
-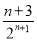 ,
,
所以Tn=3-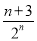 ,
,
Tn-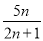 =3-
=3-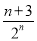 -
-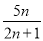
= ,
,
于是确定Tn与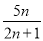 的大小关系等价于比较2n与2n+1的大小,
的大小关系等价于比较2n与2n+1的大小,
由2<2×1+1;22<2×2+1;23>2×3+1;24>2×4+1;25>2×5+1;…
可猜想当n≥3时,2n>2n+1,证明如下:
方法一:①当n=3时,对上式验算显示成立.
②假设当n=k时成立,则n=k+1(k≥2)时,
2k+1=2·2k>2(2k+1)=4k+2=2(k+1)+1+(2k-1)>2(k+1)+1,
所以当n=k+1时猜想也成立.
综合①②可知,对一切n≥3的正整数,都有2n>2n+1.
方法二:当n≥3时,
2n=(1+1)n=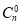 +
+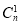 +
+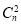 +…+
+…+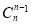 +
+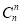 ≥
≥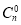 +
+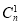 +
+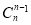 +
+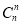 =2n+2>2n+1,
=2n+2>2n+1,
综上所述,当n≥3时,Tn>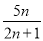 .
.
(3)因为cn=3n+ =3n+(-1)n-1λ·2n,
=3n+(-1)n-1λ·2n,
所以cn+1-cn=[3n+1+(-1)nλ·2n+1]-[3n+(-1)n-1λ·2n]
=2·3n-3λ(-1)n-1·2n>0,
所以(-1)n-1·λ<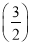 n-1.①
n-1.①
当n=2k-1(k=1,2,3,…)时,①式即为λ< 2k-2,②
2k-2,②
依题意,②式对k=1,2,3,…都成立,所以λ<1,
当n=2k,k=1,2,3,…时,①式即为λ>- 2k-1,③
2k-1,③
依题意,③式对k=1,2,3,…都成立,
所以λ>-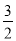 ,所以-
,所以-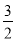 <λ<1,又λ≠0,
<λ<1,又λ≠0,
所以存在整数λ=-1,使得对任意n∈N*有cn+1>cn.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:选择题
小王从甲地到乙地往返的时速分别为a和b(a<b),其全程的平均时速为v,则( )
A.a<v< B.v=
B.v=
C. <v<
<v< D.v=
D.v=
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:选择题
在正三棱柱ABC—A1B1C1中,D是AC的中点,AB1⊥BC1,则平面DBC1与平面CBC1所成的角为( )
A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 概率与统计(解析版) 题型:填空题
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示.

(1)直方图中x的值为________;
(2)在这些用户中,用电量落在区间[100,250)内的户数为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 数列、推理与证明(解析版) 题型:填空题
(2013·淄博模拟)如图,一个类似杨辉三角的数阵,请写出第n(n≥2)行的第2个数为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 数列、推理与证明(解析版) 题型:选择题
已知向量a、b的夹角为120°,且|a|=|b|=4,那么b·(2a+b)的值为( )
A.48 B.32 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量(解析版) 题型:填空题
若非零向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为________.
查看答案和解析>>
科目:高中数学 来源:2014年吉林省延边州高考复习质量检测文科数学试卷(解析版) 题型:填空题
设△ABC的三个内角A、B、C所对的三边分别为a,b,c,若△ABC的面积为S=a2-(b-c)2,则 = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com