
点M、N分别是正方体ABCD—A1B1C1D1的棱A1B1、A1D1的中点,用过A、M、N和D、N、C1的两个截面截去正方体的两个角后得到的几何体如下图,则该几何体的正(主)视图、侧(左)视图、俯视图依次为( )


A.①②③ B.②③④
C.①③④ D.②④③
 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:填空题
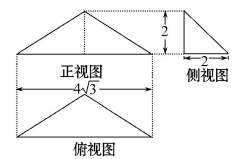
(2014·宁波模拟)已知某几何体的三视图如图所示,则该几何体的体积为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 解析几何(解析版) 题型:填空题
l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:解答题
在△ABC中,角A,B,C所对边的边长分别是a,b,c.
(1)若c=2,C= 且△ABC的面积等于
且△ABC的面积等于 ,求cos(A+B)和a,b的值;
,求cos(A+B)和a,b的值;
(2)若B是钝角,且cos A= ,sin B=
,sin B= ,求sin C的值.
,求sin C的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:选择题
在正三棱柱ABC—A1B1C1中,D是AC的中点,AB1⊥BC1,则平面DBC1与平面CBC1所成的角为( )
A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 概率与统计(解析版) 题型:解答题
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
品牌 | 甲 |
|
| 乙 |
|
首次出现故障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
轿车数量(辆) | 2 | 3 | 45 | 5 | 45 |
每辆利润(万元) | 1 | 2 | 3 | 1.8 | 2.9 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率;
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列;
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 概率与统计(解析版) 题型:填空题
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示.

(1)直方图中x的值为________;
(2)在这些用户中,用电量落在区间[100,250)内的户数为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 数列、推理与证明(解析版) 题型:填空题
(2013·淄博模拟)如图,一个类似杨辉三角的数阵,请写出第n(n≥2)行的第2个数为________.

查看答案和解析>>
科目:高中数学 来源:2014年吉林省延边州高考复习质量检测理科数学试卷(解析版) 题型:填空题
.给出下列命题:
① 已知线性回归方程 ,当变量
,当变量 增加2个单位,其预报值平均增加4个单位;
增加2个单位,其预报值平均增加4个单位;
② 在进制计算中, ;
;
③ 若 ,且
,且 ,则
,则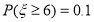 ;
;
④ “ ”是“函数
”是“函数 的最小正周期为4”的充要条件;
的最小正周期为4”的充要条件;
⑤ 设函数 的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
的最大值为M,最小值为m,则M+m=4027,其中正确命题的个数是 个。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com