【题目】已知函数f（x）=m﹣|2﹣x|，且f（x+2）＞0的解集为（﹣1，1）．
（1）求m的值；
（2）若正实数a，b，c，满足a+2b+3c=m．求 
的最小值．
【答案】
（1）解：因为f（x+2）=m﹣|x|
所以由f（x+2）＞0得|x|＜m
由|x|＜m有解，得m＞0，且其解集为（﹣m，m）
又不等式f（x+2）＞0解集为（﹣1，1），故m=1
（2）解：由（1）知a+2b+3c=1，又a，b，c是正实数，
由柯西不等式得 
当且仅当 
时取等号
故 
的最小值为9．
【解析】（1）由f（x+2）＞0得|x|＜m，求出解集，利用f（x+2）＞0的解集为（﹣1，1），求m的值；（2）由（1）知a+2b+3c=1，利用柯西不等式即可求 的最小值．
【考点精析】掌握二维形式的柯西不等式是解答本题的根本，需要知道二维形式的柯西不等式：
当且仅当
时，等号成立．
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴，建立极坐标系，若直线l的参数方程为 
（t为参数，α为l的倾斜角），曲线E的极坐标方程为ρ=4sinθ．射线θ=β，θ=β+ 
，θ=β﹣ 与曲线E分别交于不同于极点的三点A、B、C．
（1）求证：|OB|+|OC|= 
|OA|；
（2）当β= 
时，直线l过B、C两点，求y0与α的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于下列说法正确的是（ ）
A.若f（x）是奇函数，则f（x）是单调函数
B.命题“若x2﹣x﹣2=0，则x=1”的逆否命题是“若x≠1，则x2﹣x﹣2=0”
C.命题p：?x∈R，2x＞1024，则￢p：?x0∈R， 
D.命题“?x∈（﹣∞，0），2x＜x2”是真命题
查看答案和解析>>
科目：高中数学 来源： 题型：
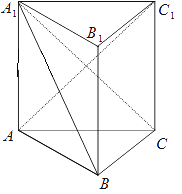
【题目】如图，三棱柱ABC﹣A1B1C1中，AA1⊥平面ABC，AA1=AC=2BC，∠ACB=90°．
（Ⅰ）求证：AC1⊥A1B；
（Ⅱ）求直线AB与平面A1BC所成角的正切值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图长方体
中，
，
分别为棱
，
的中点
（1）求证:平面
平面
；
（2）请在答题卡图形中画出直线
与平面
的交点
（保留必要的辅助线），写出画法并计算
的值（不必写出计算过程）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分
分）
已知圆
，过点
作直线
交圆
于
、
两点．
（Ⅰ）当
经过圆心
时，求直线
的方程．
（Ⅱ）当直线
的倾斜角为
时，求弦
的长．
（Ⅲ）求直线
被圆
截得的弦长
时，求以线段
为直径的圆的方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
