
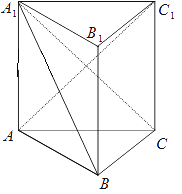
【题目】如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AA1=AC=2BC,∠ACB=90°.
(Ⅰ)求证:AC1⊥A1B;
(Ⅱ)求直线AB与平面A1BC所成角的正切值.
【答案】(1)见解析(2) ![]()
【解析】分析:(1)先证![]() 平面
平面![]() ,得到
,得到![]() ,由四边形
,由四边形![]() 为正方形得出
为正方形得出![]() ,所以
,所以![]() 平面
平面![]() ,进而证得
,进而证得![]() ;
;
(2)由![]() 平面
平面![]() 可得
可得![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,设
所成的角,设![]() ,利用勾股定理求出
,利用勾股定理求出![]() ,即可得出
,即可得出![]() 的值.
的值.
详解:证明(Ⅰ)∵CC1⊥平面ABC,BC平面ABC,
∴CC1⊥BC
又∠ACB=90°,即BC⊥AC,又AC∩CC1=C,
∴BC⊥平面A1C1CA,又AC1平面A1C1CA,
∴AC1⊥BC.
∵AA1=AC,∴四边形A1C1CA为正方形,
∴AC1⊥A1C,又AC1∩BC=C,
∴AC1⊥平面A1BC,又A1B平面A1BC,
∴AC1⊥A1B.
(Ⅱ)设AC1∩A1C=O,连接BO.
由(Ⅰ)得AC1⊥平面A1BC,
∴∠ABO是直线AB与平面A1BC所成的角.
设BC=a,则AA1=AC=2a,
∴ ![]() ,
, ![]() ,
,
在Rt△ABO中, ![]() ,
,
∴直线AB与平面A1BC所成角的正切值为 ![]() .
.


科目:高中数学 来源: 题型:
【题目】某市食品药品监督管理局开展2019年春季校园餐饮安全检查,对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如下表所示:
中学编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
卫生标准评分y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;(精确到0.1)
(2)现从8个被检查的中学食堂中任意抽取两个组成一组,若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分,则组成“对比标兵食堂”,求该组被评为“对比标兵食堂”的概率.
参考公式: ,
,![]() ;
;
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足:对任意的实数
满足:对任意的实数![]() ,存在非零常数
,存在非零常数![]() ,都有
,都有![]() 成立.
成立.
(1)当![]() 时,若
时,若![]() ,
, ![]() ,求函数
,求函数![]() 在闭区间
在闭区间![]() 上的值域;
上的值域;
(2)设函数![]() 的值域为
的值域为![]() ,证明:函数
,证明:函数![]() 为周期函数.
为周期函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|2﹣x|,且f(x+2)>0的解集为(﹣1,1).
(1)求m的值;
(2)若正实数a,b,c,满足a+2b+3c=m.求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式,并用定义法证明
的解析式,并用定义法证明![]() 在
在![]() 单调递增;
单调递增;
(3)已知![]() ,设P:
,设P:![]() ,不等式
,不等式![]() 恒成立,Q:
恒成立,Q:![]() 时,
时,![]() 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的![]() 的集合记为A,满足Q成立的
的集合记为A,满足Q成立的![]() 集合记为B,求
集合记为B,求![]() (R为全集)。
(R为全集)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足an+1+(-1)n an =2n-1,则{an}的前64项和为( )
A. 4290 B. 4160 C. 2145 D. 2080
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com