
(本小题满分12分)已知函数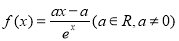 .
.
(1)当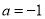 时,求函数
时,求函数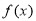 的极值;
的极值;
(2)若函数 没有零点,求实数
没有零点,求实数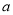 的取值范围.
的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年江苏省常州市高三上学期期末调研测试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)设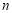 个正数
个正数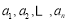 满足
满足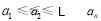 (
(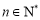 且
且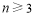 ).
).
(1)当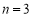 时,证明:
时,证明: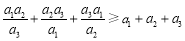 ;
;
(2)当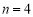 时,不等式
时,不等式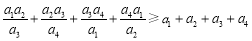 也成立,请你将其推广到
也成立,请你将其推广到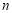 (
(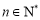 且
且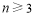 )个正数
)个正数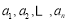 的情形,归纳出一般性的结论并用数学归纳法证明.
的情形,归纳出一般性的结论并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年贵州省贵阳市高三上学期期末监测考试文科数学试卷(解析版) 题型:填空题
某学生在复习函数内容时,得出如下一些结论:
①函数 在
在 上有最大值
上有最大值 ;
;
②函数 在
在 上是减函数;
上是减函数;
③ ,使函数
,使函数 为奇函数;
为奇函数;
④对数函数具有性质“对任意实数 ,
, ,满足
,满足 ”
”
其中正确的结论是_______.(填写你认为正确结论的序号)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省龙岩市非一级达标校高三上学期期末检查理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知函数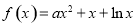 (
(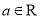 ).
).
(1)当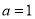 时,求函数
时,求函数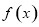 的图象在点
的图象在点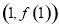 处的切线方程;
处的切线方程;
(2)设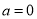 ,求证:当
,求证:当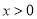 时,
时,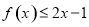 ;
;
(3)若函数 恰有两个零点
恰有两个零点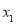 ,
,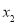 (
(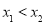 ),求实数
),求实数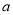 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com