
分析 (1)容易求出$\overrightarrow{m}•\overrightarrow{n}=sin(A+B)=sin2C$,进而得到sinC=sin2C,从而求得cosC=$\frac{1}{2}$,根据C的范围即可得出$C=\frac{π}{3}$;
(2)先得到$\overrightarrow{CD}=\frac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})$,而根据条件及基本不等式可得到$|\overrightarrow{CA}||\overrightarrow{CB}|≤1$,从而${\overrightarrow{CD}}^{2}=\frac{1}{4}(\overrightarrow{CA}+\overrightarrow{CB})^{2}$,进行数量积的运算,并由完全平方公式可得到${\overrightarrow{CD}}^{2}$=$1-\frac{1}{4}|\overrightarrow{CA}||\overrightarrow{CB}|$,从而可以求出${\overrightarrow{CD}}^{2}≥\frac{3}{4}$,进而即可求出$|\overrightarrow{CD}|$的最小值.
解答 解:(1)$\overrightarrow{m}•\overrightarrow{n}=sinAcosB+cosAsinB=sin(A+B)=sin2C$;
A+B=π-C,0<C<π;
∴sin(A+B)=sinC=sin2C;
∴sinC=2sinCcosC;
∴$cosC=\frac{1}{2}$,C=$\frac{π}{3}$;
(2)$\overrightarrow{CD}=\frac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})$,且$|\overrightarrow{CA}|+|\overrightarrow{CB}|=2$;
∴$|\overrightarrow{CA}||\overrightarrow{CB}|≤(\frac{|\overrightarrow{CA}|+|\overrightarrow{CB}|}{2})=1$;
∴${\overrightarrow{CD}}^{2}=\frac{1}{4}(|{\overrightarrow{CA}|}^{2}+|\overrightarrow{CA}||\overrightarrow{CB}|+|\overrightarrow{CB}{|}^{2})$
=$\frac{1}{4}(|\overrightarrow{CA}|+|\overrightarrow{CB}|)^{2}-\frac{1}{4}|\overrightarrow{CA}||\overrightarrow{CB}|$
=$1-\frac{1}{4}|\overrightarrow{CA}||\overrightarrow{CB}|$
$≥1-\frac{1}{4}$
=$\frac{3}{4}$;
∴$|\overrightarrow{CD}|≥\frac{\sqrt{3}}{2}$;
即$|\overrightarrow{CD}|$的最小值为$\frac{\sqrt{3}}{2}$.
点评 考查向量数量积的坐标运算,向量数量积的计算公式,两角和的正弦公式,以及完全平方公式,基本不等式,以及不等式的性质.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
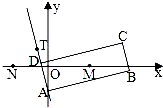 如图矩形ABCD两条对角线相交于M(2,0),AB边所在直线方程为x-3y-6=0,点T(-1,1)在AD边所在直线上,
如图矩形ABCD两条对角线相交于M(2,0),AB边所在直线方程为x-3y-6=0,点T(-1,1)在AD边所在直线上,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
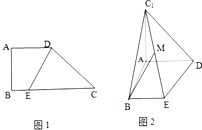 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=$\frac{1}{2}$BC=1,E是底边BC上的一点,且EC=3BE.现将△CDE沿DE折起到△C1DE的位置,得到如图2所示的四棱锥C1-ABED,且C1A=AB.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=$\frac{1}{2}$BC=1,E是底边BC上的一点,且EC=3BE.现将△CDE沿DE折起到△C1DE的位置,得到如图2所示的四棱锥C1-ABED,且C1A=AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com