
分析 根据题意列出方程,利用同角的三角函数关系式求出sinθ、cosθ与tanθ的值,再求tan(θ-$\frac{π}{4}$)的值.
解答 解:复数z=(sinθ-$\frac{3}{5}$)+(cosθ-$\frac{4}{5}$)i在复平面内的对应点在虚轴负半轴上,
∴$\left\{\begin{array}{l}{sinθ-\frac{3}{5}=0}\\{cosθ-\frac{4}{5}<0}\end{array}\right.$,
解得sinθ=$\frac{3}{5}$,cosθ=-$\frac{4}{5}$,
∴tanθ=-$\frac{3}{4}$;
∴tan(θ-$\frac{π}{4}$)=$\frac{tanθ-tan\frac{π}{4}}{1+tanθtan\frac{π}{4}}$=$\frac{-\frac{3}{4}-1}{1+(-\frac{3}{4})×1}$=-7.
故答案为:-7.
点评 本题主要考查复数的概念与应用问题,也考查了复数与复平面内对应点之间的关系问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
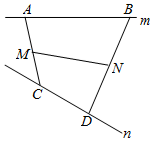 如图,已知m,n是异面直线,点A,B∈m,且AB=6,点C,D∈n,且CD=4,若M,N分别是AC,BD的中点,MN=2$\sqrt{2}$,则m与n所成角的余弦值是$\frac{5}{12}$.
如图,已知m,n是异面直线,点A,B∈m,且AB=6,点C,D∈n,且CD=4,若M,N分别是AC,BD的中点,MN=2$\sqrt{2}$,则m与n所成角的余弦值是$\frac{5}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
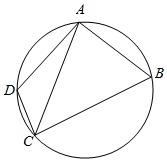 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com