在平面直角坐标系
中，以
为极点，
轴非负半轴为极轴建立坐标系，已知曲线
的极坐标方程为
，直线
的参数方程为: 
（
为参数），两曲线相交于
两点. 求：
（1）写出曲线的直角坐标方程和直线的普通方程；
（2）若
求
的值.
（1）
，
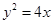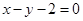；（2）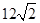
解析试题分析：（1）将曲线C的方程两边分别乘以
，再利用极坐标与直角坐标互化公式即可将极坐标方程化为直角坐标方程，对直线
方程，消去参数t,即可化为普通方程；（2）将直线的参数方程代入曲线C的直角坐标方程，化为关于t二次方程，利用根与系数关系及参数t的几何意义，即可求出|PM|+|PN|的值.
试题解析：(1)曲线C的直角坐标方程为，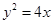
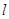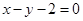直线的普通方程. 6分
(2)直线的参数方程为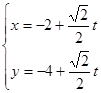
(t为参数),
代入y2=4x, 得到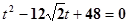
,设M,N对应的参数分别为t1,t2
则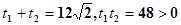
所以|PM|+|PN|=|t1+t2|=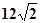
14分
考点：直角坐标方程与参数方程的互化；极坐标方程与直角坐标方程互化；直线的参数方程中参数的意义；直线与抛物线的位置关系.
活力课时同步练习册系列答案科目：高中数学 来源： 题型：解答题
在直角坐标系xOy中，直线l的方程为x﹣y+4=0，曲线C的参数方程为
（α为参数）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，
），判断点P与直线l的位置关系；
（2）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
曲线C的极坐标方程为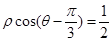
，以极点O为原点，极轴Ox为x的非负半轴，保持单位长度不变建立直角坐标系xoy.
（1）求曲线C的直角坐标方程；
（2）直线l的参数方程为
．若C与
的交点为P，求点P与点A（-2,0）的距离|PA|.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在直角坐标系xoy中，以坐标原点为极点，x轴为极轴建立极坐标系，半圆C的极坐标方程为
，
.
（1）求C的参数方程；
（2）设点D在C上，C在D处的切线与直线
垂直，根据（1）中你得到的参数方程，确定D的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在平面直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐V标方程为
，M，N分别为曲线C与x轴、y轴的交点．
（1）写出曲线C的直角坐标方程，并求M，N的极坐标；
（2）求直线OM的极坐标方程．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在直角坐标系xOy中，直线l的方程为x－y＋2＝0，
曲线C的参数方程为
(α为参数)．
（1）已知在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，点P的极坐标为
，判断点P与直线l的位置关系；
（2）设点Q是曲线C上的一个动点，求它到直线l的距离的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
以直角坐标系的原点为极点O，
轴正半轴为极轴，已知点P的直角坐标为(1,-5),点C的极坐标为
,若直线l经过点P,且倾斜角为
，圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
(坐标系与参数方程选做题)设直线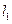
的参数方程为
（
为参数），以坐标原点为极点，x轴为极轴建立极坐标系得另一直线
的方程为
，
若直线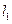与间的距离为
，则实数
的值为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的极坐标方程为
，写出曲线