
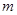 和
和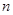 ,将
,将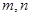 作为Q点的横、纵坐标,
作为Q点的横、纵坐标, 的夹角为
的夹角为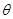 ,求
,求 的概率;
的概率; 内的概率.
内的概率.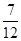 ;(2)
;(2) .
.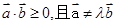 ,所以
,所以 ,所以此事件包含的基本结果共有21个,
,所以此事件包含的基本结果共有21个,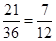 .
. 表示的平面区域可知是一个正方形,此正方形内包含横纵坐标都为正整数的点有11个,所以其概率为
表示的平面区域可知是一个正方形,此正方形内包含横纵坐标都为正整数的点有11个,所以其概率为 .
.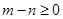 ,从而得到(1,1),(1,2),...(6,6)共36个点中有21个满足,然后根据古典概型概率计算公式计算即可.
,从而得到(1,1),(1,2),...(6,6)共36个点中有21个满足,然后根据古典概型概率计算公式计算即可. 表示的平面区域可知是一个正方形,然后找出此正方形包括边上的整点个数,再根据古典概型概率计算公式计算即可.
表示的平面区域可知是一个正方形,然后找出此正方形包括边上的整点个数,再根据古典概型概率计算公式计算即可.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:不详 题型:解答题
| 分组 | 频数 | 频率 |
 |  |  |
 |  |  |
 |  |  |
 | 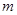 |  |
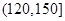 |  |  |
| 合计 |  |  |
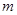 、
、 、
、 、
、 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
 分以上的人数;
分以上的人数;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,集合
,集合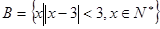 ,
,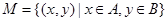
 所有可能的结果;
所有可能的结果;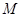 中任取一个元素,求“
中任取一个元素,求“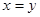 ”的概率
”的概率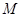 中任取一个元素,求“
中任取一个元素,求“ ”的概率.
”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
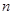 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是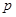 .
. 时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数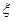 的期望
的期望 ;
; ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求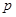 和
和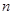 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
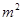 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com