练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若函数f（x）=ax4+bx2+c满足f′（1）=2，则f′（﹣1）= ．

     

    ﹣2

    【解析】

    试题分析：求导可得f′（x）=4ax3+2bx，易得函数f′（x）为奇函数，由奇函数的性质可得．

    【解析】
    ∵f（x）=ax4+bx2+c，∴f′（x）=4ax3+2bx，

    令函数g（x）=f′（x）=4ax3+2bx，

    可得g（﹣x）=﹣4ax3﹣2bx=﹣g（x），即函数g（x）为奇函数，

    ∴f′（﹣1）=﹣f′（1）=﹣2，

    故答案为：﹣2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷（解析版） 题型：填空题

    若=a+bi（i为虚数单位，a，b∈R），则a+b= ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷（解析版） 题型：解答题

    如图所示，设铁路AB=50，B、C之间距离为10，现将货物从A运往C，已知单位距离铁路费用为2，公路费用为4，问在AB上何处修筑公路至C，可使运费由A到C最省？

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 3.2导数的运算练习卷（解析版） 题型：解答题

    已知抛物线y=x2，求过点（﹣，﹣2）且与抛物线相切的直线方程．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 3.2导数的运算练习卷（解析版） 题型：填空题

    已知f（x）=x2+2x•f′（1），则f′（0）= ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷（解析版） 题型：解答题

    已知椭圆的两焦点为F1（0，﹣1）、F2（0，1），直线y=4是椭圆的一条准线．

    （1）求椭圆方程；

    （2）设点P在椭圆上，且|PF1|﹣|PF2|=1，求tan∠F1PF2的值．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷（解析版） 题型：选择题

    若双曲线x2﹣y2=1的右支上一点P（a，b）到直线y=x的距离为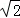，则a+b的值为（　　）

    A.﹣ B. C.± D.±2

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 2.4抛物线练习卷（解析版） 题型：填空题

    抛物线y=12x2的焦点到准线的距离为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年苏教版选修1-1 1.2简单的逻辑联结词练习卷（解析版） 题型：填空题

    已知命题p：集合{x|x=（﹣1）n，n∈N}只有3个真子集，q：集合{y|y=x2+1，x∈R }与集合{x|y=x+1}相等．则下列新命题：

    ①p或q；

    ②p且q；

    ③非p；

    ④非q．

    其中真命题的个数为 ．

     

    查看答案和解析>>

    同步练习册答案