练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某服装商场为了了解毛衣的月销售量(件)与月平均气温(℃)之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：
    月平均气温
    		17
    		13
    		8
    		2
    月销售量（件）
    		24
    		33
    		40
    		55
    （1）做出散点图；
    (2) 求线性回归方程 ；
    (3)气象部门预测下个月的平均气温约为6ºC，据此估计该商场下个月毛衣的销售量．（   ,）
    （1）
    ，（2） (3) 46件。

    试题分析：（1）
    ……2分
    （2） ,  3分
     5分
     7分
    线性回归方程为  8分
    (3)当时，，
    因此估计下月毛衣销量约为46件。10分
    点评：求回归直线方程的步骤是：①作出散点图，判断散点是否在一条直线附近；②如果散点在一条直线附近，由公式求出a、b的值，并写出线性回归方程。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:
    零件的个数x(个)
    		2
    		3
    		4
    		5
    加工的时间y(小时)
    		2.5
    		3
    		4
    		4.5
    由表中数据算出线性回归方程=bx+a中的b≈0.7,试预测加工10个零件需_______小时(已知a=-b).

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查，统计数据如下表所示
     
    		积极参加班级工作
    		不太主动参加班级工作
    学习积极性高
    		18
    		7
    学习积极性一般
    		6
    		19
    （I）如果随机抽查这个班的一名学生，那么抽到积极参加班级工作的学生的概率是多少？抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少？
    （II）试运用独立性检验的思想方法分析：学生的学习积极性与对待班级工作的态度是否有关？并说明理由
    附：
    P（≥k）
    		0.050
    		0.010
    		0.001
    		=
    k
    		3.841
    		6.635
    		10.828
     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    由一组数据(x1，y1)、(x2、y2)、 、(xn，yn)得到的线性回归方程为y＝a＋bx，则下列说法正确的是(　　)
    A．直线y＝a＋bx必过点(，)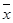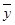
    B．直线y＝a＋bx至少经过点(x1，y1)、(x2，y2)、 、(xn，yn)中的一点
    C．直线y＝a＋bx是由(x1，y1)、(x2、y2)、 、(xn，yn)中的两点确定的
    D．(x1，y1)、(x2，y2)、 、(xn、yn)这n个点到直线y＝a＋bx的距离之和最小

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知、之间的一组数据如右表：

    		0
    		1
    		2
    		3

    		8
    		2
    		6
    		4
    则线性回归方程所表示的直线必经过点 (       )
    A．（0，0）         B．（1.5,5）         C．（4,1.5）          D．（2,2）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    根据一组样本数据的散点图分析存在线性相关关系，求得其回归方程，则在样本点处的残差为（   ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下面是2×2 列联表
     x          y
    		y 1
    		y 2
    		合计
    x1
    		a
    		21
    		73
    x2
    		2
    		25
    		27
    合计
    		b
    		46
    		100
    则表中 a 、b 处的值分别为（    ）
    A．94 、96         B．52 、50       C．52 、54       D．54 、52

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某研究机构对高三学生的记忆力x和判断力y进行统计分析，得下表数据
    x
    		6
    		8
    		10
    		12
    y
    		2
    		3
    		5
    		6
    请画出上表数据的散点图； （要求 : 点要描粗）
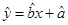    （2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；（3）试根据（II）求出的线性回归方程，预测记忆力为9的同学的判断力。
    （相关公式：）

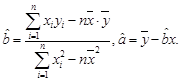    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某车间生产一种玩具,为了要确定加工玩具所需要的时间,进行了10次实验,数据如下:
    玩具个数
    		2
    		4
    		6
    		8
    		10
    		12
    		14
    		16
    		18
    		20
    加工时间
    		4
    		7
    		12
    		15
    		21
    		25
    		27
    		31
    		37
    		41
    如回归方程的斜率是，则它的截距是 (　　)
    A.＝11－22；      B.＝11－22；      C.＝22－11；      D.＝22－11.

    查看答案和解析>>

    同步练习册答案